数据表示与运算
1. 数制与编码
1.1 进制转换
二进制与十进制转换
- 二进制转十进制:按权展开求和
- 十进制转二进制:除2取余法(整数部分),乘2取整法(小数部分)
八进制与十六进制
- 八进制:每3位二进制对应1位八进制
- 十六进制:每4位二进制对应1位十六进制
| 十进制 | 二进制 | 八进制 | 十六进制 |
|---|---|---|---|
| 0 | 0000 | 0 | 0 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 15 | 1111 | 17 | F |
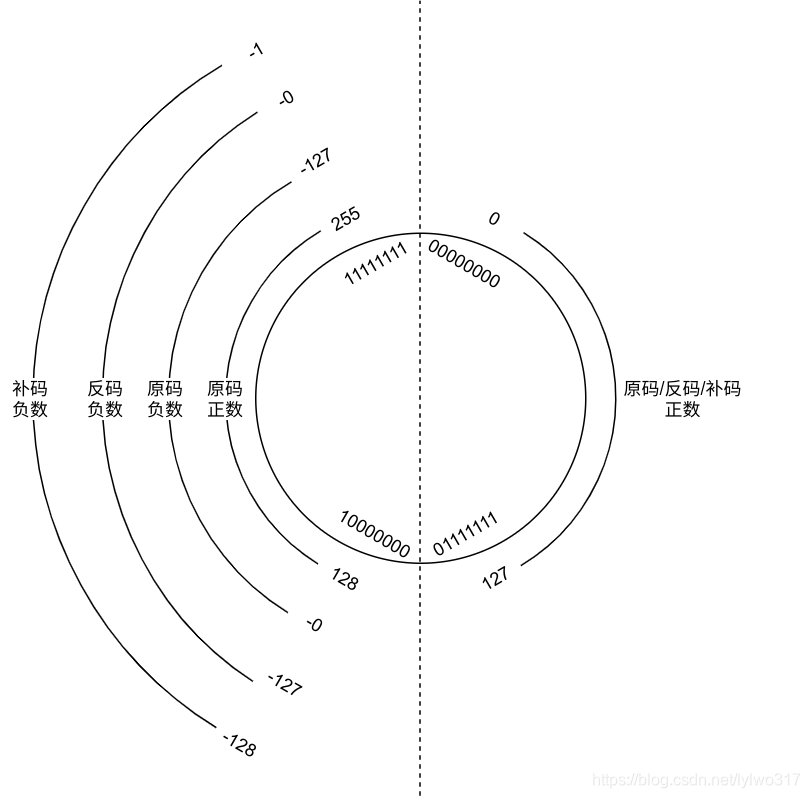
1.2 原码、反码、补码
| 数值 | 原码 | 反码 | 补码 |
|---|---|---|---|
| +7 | 0111 | 0111 | 0111 |
| -7 | 1111 | 1000 | 1001 |
原码表示法
- 正数:符号位为0,数值位不变
- 负数:符号位为1,数值位不变
- 特点:表示简单,但运算复杂
例如,对于 8 位二进制数:
- 正数 5 的原码是 00000101 ,其中最高位 0 表示正数,后面 7 位 0000101 表示数值 5 。
- 负数 -5 的原码是 10000101 ,最高位 1 表示负数,后面 7 位 0000101 表示数值 5 。
原码的优点是直观易懂,与人的日常习惯比较接近。但在进行加减法运算时,需要单独处理符号位,比较复杂。比如计算 5 + (-5) ,用原码计算时,先分别写出 5 和 -5 的原码 00000101 和 10000101 ,然后进行加法运算,得到 10001010 ,其结果是 -10 ,这显然是错误的。这就体现出原码在进行运算时的不便,所以在计算机中,更多使用补码来进行运算。
反码表示法
- 正数:与原码相同
- 负数:符号位为1,数值位按位取反
- 特点:解决了原码的运算问题,但仍有+0和-0
补码表示法
- 正数:与原码相同
- 负数:反码+1
- 特点:统一了+0和-0,运算最方便
2. 定点数运算
2.1 定点数表示
定点整数
- 纯整数:小数点固定在最低位之后
- 表示范围:-2^(n-1) 到 2^(n-1)-1
定点小数
- 纯小数:小数点固定在最高位之前
- 表示范围:-1 到 1-2^(-(n-1))
2.2 定点数运算
加法运算
- 同号相加:直接相加,注意溢出
- 异号相加:转换为减法运算
减法运算
- 转换为加法:A-B = A+(-B)
- 溢出检测:符号位变化
乘法运算
- 原码乘法:符号位单独处理
- 补码乘法:Booth算法
除法运算
- 原码除法:恢复余数法、加减交替法
- 补码除法:不恢复余数法
3. 浮点数运算
3.1 浮点数表示
IEEE 754标准
- 单精度:32位(1位符号+8位指数+23位尾数)
- 双精度:64位(1位符号+11位指数+52位尾数)
规格化
- 规格化数:尾数最高位为1
- 非规格化数:指数为0,尾数最高位为0
3.2 浮点数运算
加法运算
- 对阶:使两个数的指数相同
- 尾数相加:按定点数加法规则
- 规格化:调整结果使其符合规格化形式
- 舍入:按舍入规则处理
乘法运算
- 符号位处理:异或运算
- 指数相加:E1+E2-bias
- 尾数相乘:按定点数乘法规则
- 规格化:调整结果
- 舍入:按舍入规则处理
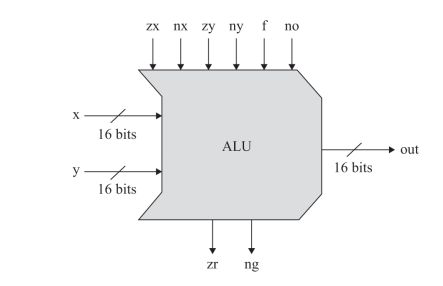
4. 算术逻辑单元(ALU)
4.1 ALU基本结构
主要组件
- 算术运算器:加法器、减法器
- 逻辑运算器:与、或、非、异或
- 移位器:左移、右移、循环移位
- 标志寄存器:进位、溢出、零标志
控制信号
- 功能选择:选择运算类型
- 数据选择:选择操作数
- 结果选择:选择输出结果
4.2 加法器设计
半加器
- 输入:A、B
- 输出:和S、进位C
- 逻辑:S=A⊕B,C=A·B
全加器
- 输入:A、B、Cin
- 输出:和S、进位Cout
- 逻辑:S=A⊕B⊕Cin,Cout=A·B+(A⊕B)·Cin
并行加法器
- 行波进位加法器:简单但速度慢
- 超前进位加法器:复杂但速度快
- 分组并行加法器:折中方案
5. 移位运算
5.1 移位类型
逻辑移位
- 左移:高位丢弃,低位补0
- 右移:低位丢弃,高位补0
算术移位
- 左移:高位丢弃,低位补0
- 右移:低位丢弃,高位补符号位
循环移位
- 左循环:高位移入低位
- 右循环:低位移入高位
5.2 移位应用
乘法运算
- 左移:相当于乘以2的幂
- 右移:相当于除以2的幂
除法运算
- 快速除法:利用移位实现
6. 总结
数据表示与运算是计算机组成原理的核心内容,涉及数制转换、定点数运算、浮点数运算等多个方面。掌握这些基本概念和运算方法对于理解计算机的运算原理具有重要意义。

