OpenLayers

在学习OpenLayers之前，我们需要学习一些空间地理的相关知识，只需要涉及一些基础的地理信息。这些知识，相信在初中地理老师已经教过我们，只是有些遗忘了而已，是时候拾起来了。

在这章中介绍经纬度相关的概念、墨卡托投影以及墨卡托投影中存在的墨卡托失真的问题。

经度与纬度

地理坐标系一般是指由经度、纬度和相对高度组成的坐标系，能够标示地球上的任何一个位置。经度和纬度常合称为经纬度。

1. 2D中的经纬度表示

2. 3D中的经纬度表示

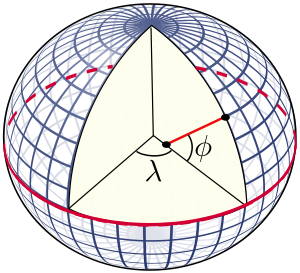
• λ：经度，线面角
• φ：纬度，二面角

纬度

纬度是指某点与地球球心的连线和地球赤道面所成的线面角，其数值在0至90度之间。简写如下

• 位于赤道以北的点的纬度叫北纬，记为N
• 位于赤道以南的点的纬度称南纬，记为S。

经度

经度是一种用于确定地球表面上不同点东西位置的地理坐标。经度是一种角度量，通常用度来表示，并被记作希腊字母λ(lambda)。

不同于纬度，可以使用赤道作为自然的起点。经度没有自然的起点而使用经过伦敦格林尼治天文台旧址的子午线作为起点。东经180°即西经180°。

按照惯例，本初子午线是经过伦敦格林威治皇家天文台 的子午线，是0度经线所在地。其他位置的经度是通过测量其从本初子午向东至180°E向西至180°W，而且东经180°即西经180°，约等同于国际日期变更线，国际日期变更线的两边，日期相差一日。

• 位于子午线以西的点的经度叫西经，记为W
• 位于子午线以东的点的纬度称东经，记为E。

具体来说，某位置的经度是一个通过本初子午线的平面和一个通过南极、北极和该位置的平面所组成的二面角。

案例1:

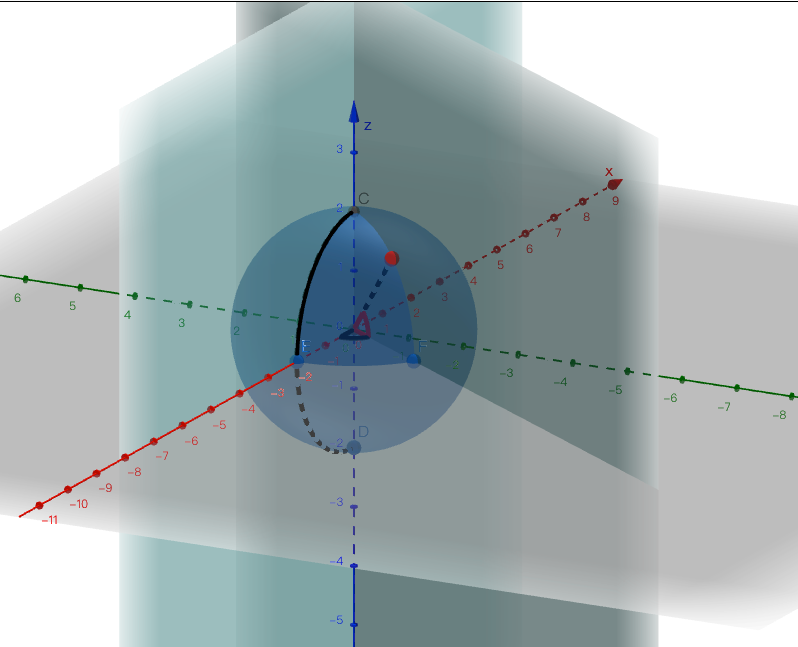
• 黑线表示本初子午线
• 红点出的经度为图中黑色夹角（二面角）
• 红点出的纬度为图中红色夹角（线面角）

INFO

此案例并不标准，因为经纬度是建模在扁椭球上的地理坐标系

转换

经度和纬度的每一度被分为60角分，每一分被分为60秒。分为3个单位，分别是度（D）、分（M）、秒（S），常见的几种表示格式如下：

• DD：40.749807, 73.983673
• DMS：40° 44´ 59.305" N 73° 59´ 1.223" E
• DM：40° 44.988416666667" , 73° 59.020383333333"

有时西经被写做负数：-23.45833°。偶尔也有人把东经写为负数，但这相当不常规。

转换方法参考如下：

const transformDMSFromDD = function(coordinate: [number, number]) {
  return coordinate.map((item, index) => {
    const D = Math.floor(item);
    const M = Math.floor((item - D) * 60);
    const S = Math.floor(((item - D) * 60 - M) * 60);
    let result = D + '°' + M + '´' + S + '\"';

    if (index === 0) {
      D > 0 ? result += 'E' : result += 'W';
      return result;
    }
    if (index === 1) {
      D > 0 ? result += 'N' : result += 'S';
      return result;
    }
  });
};

export default transformDMSFromDD;

INFO

在transformDMSFromDD转换方法中，默认数组中经度在前、纬度在后，在不同的WebGIS框架中并不相同。例如

• OpenLayers：经度在前，纬度在后
• Leaflet：则是纬度在前，经度在后

投影

为了方便制作地图，这就需要一种方法将球面上的点转换为平面上的点，球面必然会有一定程度的变形 。根据地图的目的，有些变形是可以接受的，有些则是不可以接受的，因此，为了保留球面的某些性质而牺牲其他性质，就存在不同的地图投影。

例如：

• 墨卡托投影：牺牲了等面积而保留了等角的特性，意味着3D地球中的航向角度在2D地图上的角度是相等的
• 横轴墨卡托投影（又称高斯-克吕格投影）：牺牲了等角，但是减少了面积上的变形

将3D的地球投影到2D的地图中，投影有很多种类型，但最常见的类型之一是圆柱投影 。圆柱投影是将一个圆柱面包围椭球体，并使之相切或相割，再根据某种条件将椭球面上的经纬网点投影到圆柱面上，然后，沿圆柱面的一条母线切开，将其展成平面而得到的投影。

INFO

一般来说，投影意味着降维。

圆柱投影

想象一个半透明的空心球体，里面有一盏灯。现在用一张空白的地图纸把它包起来，就像一个圆柱体：

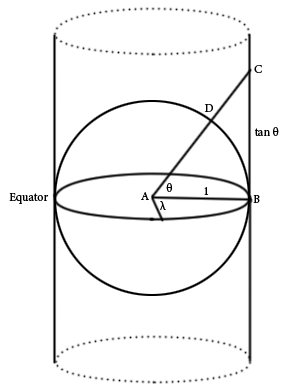
设地球为一个单位球体，经度（东西方向）记为λ，纬度（南北方向）记为φ。A为地心，B是赤道上一点。

现在将光源放置在点处A；将地球表面上的点D直线投影到圆柱体上的点C，使得点A、D和C共线。利用一些三角函数，我们得到

$$\tan \theta =\frac{BC}{AB}$$

由于AB=1， BC的长度为

$$\tan \phi$$

那么2D地图中的x轴与经度λ的关系为

$$x=\lambda$$

y轴与纬度φ的关系为

$$y=\tan \phi$$

对球体上的每个点重复此过程后，圆柱体将展开为一张平板。结果是以下地图：

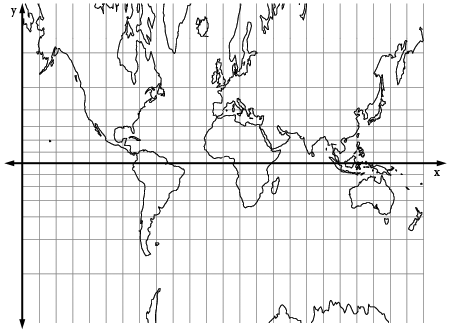
看看我们创建的地图，情况显然并非如此。地图也不保形，也不保持形状。在等角地图中，任意两条线之间的角度必须与地图上对应线的角度相同。

墨卡托投影

又称为正轴等角圆柱投影。在墨卡托地图上，所有纬线的长度都相同，纬线只是一条横跨整个地图宽度的线。但在球体地球上，纬线越靠近赤道就越长，越靠近两极就越短

许多人对墨卡托投影的工作原理存在误解：其理念是想象一个圆柱体，里面有一个球体，光线从中心穿过球体投射到圆柱体上，如图所示。然后展开圆柱体。这个圆柱投影不是墨卡托投影。

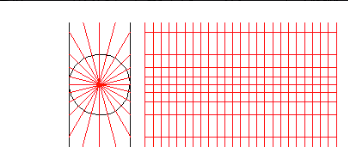
为了得到墨卡托投影的物理模型，可以让地球仪成为一个球形气球，它在圆柱体内部被吹大，并且当它与圆柱体接触时会粘在圆柱体上。

墨卡托地图上的直线在地球上并不是笔直的而是一个曲线，又称为恒向线，也就意味着在确定航向之后，按着相同方位前进即可到达目的地。

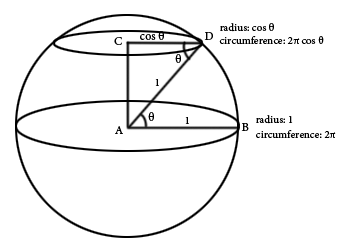
设地球是一个以A为中心的单位球体。D是地球表面的一点，B是在赤道上一点。CD平行于AB，并且AC垂直与AB。因为AB=1，地球赤道处的周长是2πR。但纬度φ上的周长只有

$$2\mathrm{\Pi }R\cos \phi$$

由于AB平行与CD，则有

$$\cos \phi =\frac{CD}{AD}=\frac{CD}{1}=CD$$

在地图上，赤道的长度与纬线φ处的长度是相等等。但在地球上，纬度φ的纬线比赤道小。在投影中，任何纬度线最终都会被水平拉伸1/cosφ 或secφ倍。

为了满足保角性，地图的任何部分水平拉伸某个因子（例如k），都必须垂直拉伸相同的因子。这样做可以保留地图该部分的角度：

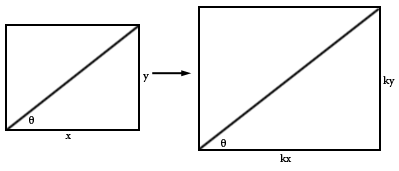
但这只有在这块土地没有面积时才有效。但对于任意土地无论多小都有一定面积，因此这块土地的纬度不是$\theta$，而是从$\theta$到$\theta +\mathrm{\Delta }\theta$其中是某个增量$\mathrm{\Delta }\theta$。同样，这块土地在地图上占据的空间不仅仅是是，而是从$y$到$y+\mathrm{\Delta }y$其中 是某个增量 $\mathrm{\Delta }y$。现在当$\mathrm{\Delta }\theta$趋近于0时，$\mathrm{\Delta }y/\mathrm{\Delta }\theta$的比率趋近于：$\sec \theta$

$$\underset{\mathrm{\Delta }\theta \to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }\theta }=\sec \theta$$

或者等价于

$$\frac{dy}{d\theta }=\sec \theta$$$$\begin{array}{rl}y& =\int \sec \theta d\theta \\ & =\int (\sec \theta \cdot \frac{\sec \theta +\tan \theta }{\sec \theta +\tan \theta })d\theta \\ & =\int \frac{{\sec }^2\theta +\sec \theta \tan \theta }{\sec \theta +\tan \theta }d\theta \end{array}$$

如果我们设$u$为分母，$u=\sec \theta +\tan \theta$则分子是的导数$u$，或$du={\sec }^2\theta +\sec \theta \tan$ \theta。因此我们可以代$u$入积分：

$$\begin{array}{rl}y& =\int \frac{du}{u}\\ & =\ln |u|+C\\ & =\ln |\sec \theta +\tan \theta |+C\end{array}$$

我们定义了地图，使得赤道位于 x 轴上，因此当 时$\theta =0$，$y=0$。代入并解$C$，我们发现$C=0$。此外，由于$\sec \theta +\tan \theta >0$对于$-\frac{\pi }{2}<\theta <\frac{\pi }{2}$，我们可以删除绝对值括号。因此:

$$y=\ln （\sec \theta +\tan \theta ）$$

Web墨卡托投影

EPSG:3857

Web墨卡托投影是墨卡托投影的一种变体，被Web地图应用业界普遍采纳。Web墨卡托是墨卡托投影地图的一个轻微变体，主要用于基于Web的地图程序。对于小比例尺地图，它与标准的墨卡托用的公式一样。但Web墨卡托在所有比例尺下都使用球面公式，但大比例尺的墨卡托地图通常使用投影的椭球面形式。

人们普遍对Web墨卡托与标准墨卡托的不同认识不足，导致了相当多的混乱和误用，错误转换造成的误差在地面上可以达到40 km。

Web墨卡托的公式与标准球面墨卡托的公式基本相同，但是在应用缩放之前，将“世界坐标”调整为使得左上角为(0, 0)，右下角为(256, 256)：[8]

$${\displaystyle \begin{array}{rl}x& =\lfloor \frac{256}{2\pi }{2}^{\text{zoom level}}(\lambda +\pi )\rfloor \text{ pixels}\\ y& =\lfloor \frac{256}{2\pi }{2}^{\text{zoom level}}(\pi -\ln [\tan (\frac{\pi }{4}+\frac{\phi }{2})])\rfloor \text{ pixels}\end{array}}$$

其中 λ 是用弧度表示的经度，而 φ 是用弧度表示的大地纬度。

拓展

缩放比例尺计算

对于小比例地图，椭球体近似为半径为 a 的球体，其中 a 约为 6,371 公里。缩放后地球的半径为R，则投影的主尺度计算公式为

$$RF=\frac{a}{R}$$

例如，书中印刷的墨卡托地图的赤道宽度可能为 13.4 厘米，对应的地球半径为 2.13 厘米， 则RF约为1/3M （M是 1,000,000的缩写）

参考：

【1】 notes-on-mercators-projection

【2】 mercator

【3】 Mercator_projection_transformations

【4】 墨卡托投影-wiki

【5】 wilhelmkruecken

【6】 Web_Mercator_projection