函数

• 函数的三要素：定义域-x、对应法则-f、值域-y
  • 两个函数的想等条件：定义域、对应法则想等
• 函数的运算
  • 四则运算
  • 复合运算
  • 反函数
  • 基本初等函数->初等函数
• 性质：有界性、单调性、奇偶性、周期性

考点

求定义域

1. x -> wrap(x)

• 简单：通过给定的定义域（具体的值），推出给定表达式的定义域
• 中等：在简单的基础上（其中给定的定义域为抽象值），需要对范围分类讨论，最后取交集
• 困难：提高表达式的复杂度

2. 给定f(x)表达式，求x的范围

基础知识点

常考函数的限制条件：对数函数、幂函数、三角函数、反三角函数

幂函数

一般地，函数

${\displaystyle f(x)=x^a}$叫做幂函数（英语：Power function），其中 ${\displaystyle x}$是自变量（底数）， ${\displaystyle a}$是常数。

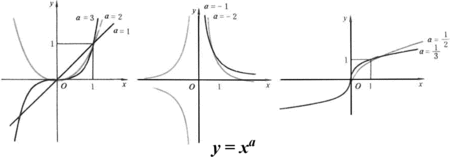
设指数为n（n为分数，则n>=0，n为负数，则n!=0）

1．第一象限内图象类型之规律（如图1）

• n＞1时，过（0，0）、（1，1）抛物线型，下凸递增。
• n＝1时，过（0，0）、（1，1）的射线。
• 0＜n＜1时，过（0，0）、（1，1）抛物线型，上凸递增。
• n＝O时，变形为y＝1（x≠0），平行于x轴的射线。
• n＜0时过（1，1），双曲线型，递减，与两坐标轴的正半轴无限接近。

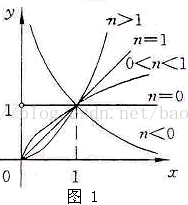
2．第一象限内图象走向之规律（如图1）

• x≥1部分各种幂函数图象，指数大的在指数小的上方；
• O＜x＜1部分图象反之，此二部分图象在（1，1）点穿越直线y＝x连成一体。

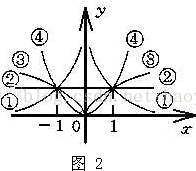
3．各个象限内图象分布之规律：设，互质，。

• 任何幂函数在第一象限必有图象，第四象限必无图象。
• n＝奇数/偶数时，函数非奇非偶，图象只在第一象限（如图1）。
• n＝偶数/奇数时，函数是偶函数、图象在第一、二象限并关于y 轴对称（如图2）。
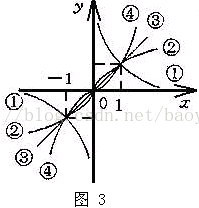
• n＝奇数/奇数时，函数是奇函数，图象在第一、三象限并关于原点对称（如图3）。

INFO

思考a为-1、1、1/2、2、3的单调性、定义域、值域、奇偶性

指数函数

对数函数

1. 图表

2. 特性

• 定义域为 ${\displaystyle (0,+\mathrm{\infty })}$，值域为${\displaystyle \mathbb{R}}$
• 必过(1,0)点

3. 运算规则

三角函数

反三角函数