直线和射线

在经典几何学中，定义线段、射线、直线

• 直线：向两个方向无限延伸
• 线段：直线的有限部分，有两个端点
• 射线：直线的“有限部分”，有一个端点

但是在计算科学和计算几何中，对射线的定义做出了修改

• 射线：有向的线段

表示方法

两点表示法

给出两个端点：起点和终点，这是最直观的表示方式

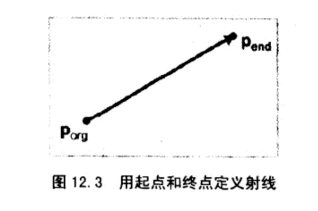
参数表示法

用两个函数在2D中表示射线的参数形式

$$\{\begin{array}{c}x(t)=x_0+t\mathrm{\Delta }x\\ y(t)=y_0+t\mathrm{\Delta }y\end{array}$$

表示3D中的射线，只需要加上z轴的即可

$$\{\begin{array}{c}x(t)=x_0+t\mathrm{\Delta }x\\ y(t)=y_0+t\mathrm{\Delta }y\\ z(t)=z_0+t\mathrm{\Delta }z\end{array}$$

其中∆x、∆y、∆z分别表示射线的方向

进而推广到任意维度的射线表示方法

$$p(t)=p_0+td,t\in (0,l)$$

• p₀是射线的起点，d是射线的方向
• 当t=0时，有p(0)=p₀
• 当t=1时，有p(1)=p₀+d

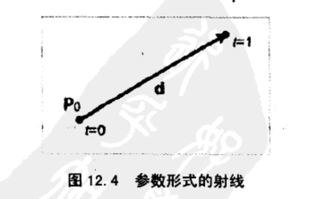
INFO

我们经常在相交性测试中，使用上述公式的一种变形

d为单位向量n，参数从0变化到l，l为射线的长度

隐式定义

在2D中定义直线

$$ax+by=d$$

在3D中定义直线，两个相交的平面确定一条直线

$$\{\begin{array}{c}{a}_{1}x+b_{1}y+c_{1}z=d_1\\ a_{2}x+b_{2}y+c_{2}z=d_2\end{array}$$

向量表示法

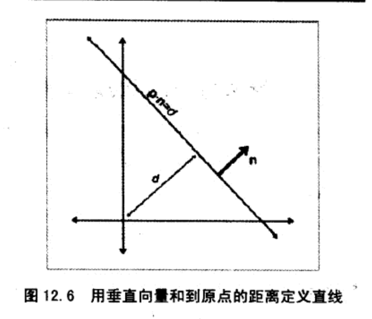
也可以转换为向量形式，其中n为[a, b]，为垂直于直线的向量（法向量）

$$pn=d$$

根据点乘的几何意义可知，任意点在单位向量n上的投影长度相等构成的集合即为直线

斜截式

在2D中定义直线

$$y=mx+b$$

水平直线的m为0，垂直直线的m无穷大，因而无法用斜截式表示。总之，直线越陡，斜率越大

其他表示方法

直线的垂直方向上的向量，根据距离原点的距离来确定直线

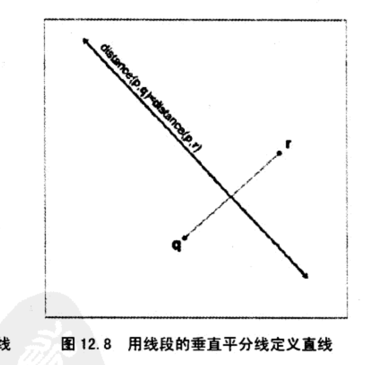
也可以将直线作为两个点构成线段的垂直平分线，直线上的点构成到这两点距离相等的几何

参考

【1】参数曲线

【2】空间三维直线方程求解方法