两条隐式直线的相交性检测
分为在2D和3D的情况
2D
2D中的相交性检查比较简单,联立方程组求解即可
求得相交点的表达式
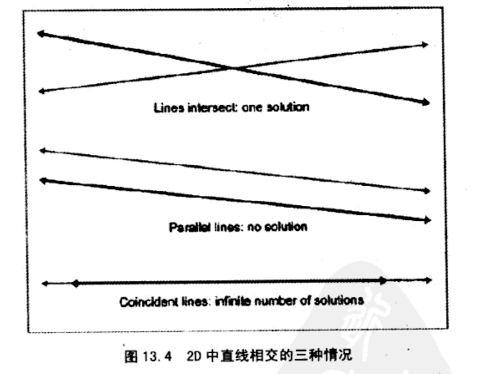
- 只有一个解,意味着只有一个交点
- 有无穷多个解,分母为0,意味着两条直线重合
- 没有解,分母为0,意味着两条直线平行
3D
在3D中有两条射线,分别是r1、r2
为了具有一般性,我们不限制t的范围,也不限制d为单位向量。
相对于2D中的直线相交性检查,3D中会存在两个直线不再同一个平面上,所有有以下4种情况
- 在同一个平面上
- 两条射线交与一点
- 两条射线平行
- 两条射线重合
- 不在同一个平面上
那么在3D中两条射线的交点有
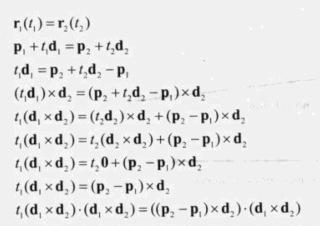
- 两条射线平行或重合,d1、d2的叉乘为0,相应的分母为0
- 如果两条射线不在一个平面,那么p1(t1)、p2(t2)是相距最近的点
上述讨论并没有限制射线的长度,如果有长度限制,那么需要做适当的边界检查

