矩阵

向量是标量的数组，矩阵是向量的数组。可以将向量看作是1xn或者nx1的矩阵

$$\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$$$$\left[\begin{array}{ccc}1& 2& 3\end{array}\right]$$

一个m行、n列的矩阵示例

$$\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]$$

方阵

行数与列数相等，表现为一个正方形矩阵，主要讨论2x2，3x3，4x4矩阵

$$\left[\begin{array}{ccc}1& 2& 3\\ 1& 2& 3\\ 1& 2& 3\end{array}\right]$$

对角矩阵

行号与列号相等的元素称为对角线元素，如果一个矩阵只有对角线元素有值，其他位置的元素值为0，那么这个矩阵称为对角矩阵。

$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 2& 0\\ 0& 0& 3\end{array}\right]$$

单位矩阵

单位矩阵是一种特殊的对角矩阵，对角线元素的值均为1

$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

单位矩阵的基本性质是：任意矩阵乘单位矩阵都会得到原矩阵

矩阵转置

一个m x n的矩阵M转置之后，变为n x m的矩阵

$${\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]}^T=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{m1}\\ a_{12}& a_{22}& \cdots & a_{m2}\\ ⋮& ⋮& \ddots & ⋮\\ a_{1n}& a_{2n}& \cdots & a_{mn}\end{array}\right]$$

转置记法经常在书面中表示列向量

引理：

• 对于任意矩阵，转置两次之后都会得到原矩阵
• 任意对角矩阵，转置之后仍是自身

矩阵乘法

与标量相乘

标量与矩阵中的元素挨个相乘

$$k\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]k=\left[\begin{array}{cccc}k{a}_{11}& k{a}_{12}& \cdots & k{a}_{1n}\\ k{a}_{21}& k{a}_{22}& \cdots & k{a}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ k{a}_{m1}& k{a}_{m2}& \cdots & k{a}_{mn}\end{array}\right]$$

与矩阵相乘

在进行矩阵乘法运算之前，首先需要判断矩阵乘法是否有意义：

一个m x n的矩阵，与r x c的矩阵相乘时，只有当n = r时乘法才有意义，最终得到一个m x c的矩阵。

$$c_{ij}=\sum _{k=1}^n{a}_{ik}{b}_{kj}$$

矩阵c中第i行、第j列的元素值是矩阵a第i行的向量与矩阵b第j列向量的点乘，推广可知矩阵c中的每个元素的值是矩阵a对应行向量和矩阵b对应列向量的点乘。

为了更好的记忆计算规则，在计算时可以将乘数位置的矩阵放在上面，方便计算。

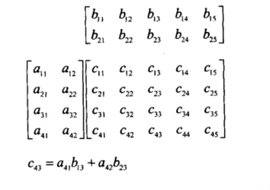
注意事项

1. 矩阵乘法不满足交换律

$$AB\ne BA$$

WARNING

如果方阵是单位矩阵，则结果为原矩阵

$$AI=IA=A$$

2. 矩阵乘法满足结合律

$$ABC=A(BC)=(AB)C$$

INFO

前提是ABC相乘是有意义的，而且如果AB有意义，那么BC也一定有意义。

3. 矩阵与标量的乘法也满足结合律

$$kA=Ak$$

4. 矩阵转置

$$(AB{)}^T=B^T{A}^T$$

推广到n个矩阵的转置

$$(M_1{M}_2\cdots M_{n-1}{M}_n{)}^T=M_n^T{M}_{n-1}^T\cdots M_2^T{M}_1^T$$

向量与矩阵的乘法

行向量左乘矩阵有意义，列向量右乘矩阵有意义。（左乘和右乘是根据向量的位置判断的，向量在左边则为左乘，在右边则为右乘）

在几何上解释pM、Mp

• 左乘相当于对矩阵M的行向量进行转换
• 右乘相当于对矩阵M的列向量进行转换

简称为左乘行右乘列

几何解释

每个矩阵都代表着一种坐标系的变换，但是我们在需要对图形进行线性变换时，如何构建这个矩阵是要研究的问题。线性变换在保持直线的同时，其他几何性质，例如：体积、面积、长度、角度可能会在变换后改变。线性变换不包含平移，仿射变换包含平移

下面是一些有用的变换：

• 旋转
• 放缩
• 投影
• 镜像
• 仿射

以三维坐标系为例，存在向量v：

$$v=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=x\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]+y\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]+z\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$$

可以进一步推广

$$p=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$$$$q=\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$$$$r=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$$$$v=xp+yq+zr$$

由此可知，任意向量都可以拆分为对应坐标轴基向量的线性组合

继续推广到更一般的情况

$$p=\left[\begin{array}{c}{p}_x\\ p_y\\ p_z\end{array}\right]$$$$q=\left[\begin{array}{c}{q}_x\\ q_y\\ q_z\end{array}\right]$$$$r=\left[\begin{array}{c}{r}_x\\ r_y\\ r_z\end{array}\right]$$$$\begin{array}{rl}\left[\begin{array}{ccc}x& y& z\end{array}\right]\left[\begin{array}{ccc}{p}_x& p_y& p_z\\ q_x& q_y& q_z\\ r_x& r_y& r_z\end{array}\right]& \\ & =\left[\begin{array}{ccc}x{p}_x+y{q}_x+z{r}_x& x{p}_y+y{q}_y+z{r}_y& x{p}_z+y{q}_z+z{r}_z\end{array}\right]& & \\ & =\left[\begin{array}{ccc}x{p}_x& x{p}_y& x{p}_z\end{array}\right]+\left[\begin{array}{ccc}y{q}_x& y{q}_y& y{q}_z\end{array}\right]+\left[\begin{array}{ccc}z{r}_x& z{r}_y& z{r}_z\end{array}\right]& \\ & =xp+yp+zr\end{array}$$

这与前面计算结果相同，因此如果我们将对角矩阵中的每个行向量看作是线性变换后坐标系的基向量，那么对角矩阵代表的是将原坐标系下的向量变换为新坐标系下的向量

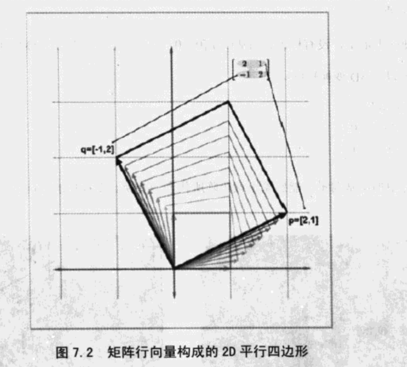
2D

$$\left[\begin{array}{cc}2& 1\\ -1& 2\end{array}\right]$$

可以得到转换后坐标系下的两个基向量：

$$\left[\begin{array}{cc}2& 1\end{array}\right]$$$$\left[\begin{array}{cc}-1& 2\end{array}\right]$$

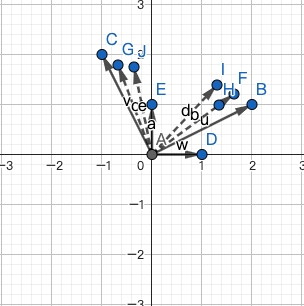
那么该矩阵可以看作是两个变换的组合：旋转、放大

3D

考虑以下3D转换矩阵：

$$\left[\begin{array}{ccc}0.707& -0.707& 0\\ 1.250& 1.250& 0\\ 0& 0& 1\end{array}\right]$$

总结：

1. 矩阵可以看作对原坐标系的基向量的一种线性变换
2. 方阵的行向量可以看作是转换后坐标系的基向量，这也恰好可以用来计算转换矩阵，只需要计算坐标系转换后的基向量即可
3. 推广到多维矩阵与多维矩阵相乘，其几何意义是将左边矩阵的列向量转换到以右边矩阵``行向量为基向量的坐标系中