行列式

在任意方阵都有一个标量，这个变量成为该方阵的行列式，用|M|表示行列式。

代数计算

2D

$$\left|\begin{array}{c}M\end{array}\right|=\left|\begin{array}{cc}{m}_{11}& m_{12}\\ m_{21}& m_{22}\end{array}\right|=m_{11}{m}_{22}-m_{12}{m}_{21}$$

可以用以下方便记忆

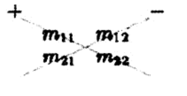
3D

$$\begin{array}{rl}\left|\begin{array}{c}M\end{array}\right|& \\ & =\left|\begin{array}{ccc}{m}_{11}& m_{12}& m_{13}\\ m_{21}& m_{22}& m_{23}\\ m_{31}& m_{32}& m_{33}\end{array}\right|& \\ & =m_{11}{m}_{22}{m}_{33}+m_{12}{m}_{23}{m}_{31}+m_{13}{m}_{21}{m}_{32}-m_{31}{m}_{22}{m}_{13}-m_{21}{m}_{12}{m}_{33}-m_{32}{m}_{23}{m}_{11}\\ & =m_{11}(m_{22}{m}_{33}-m_{23}{m}_{32})+m_{12}(m_{23}{m}_{31}-m_{21}{m}_{33})+m_{13}(m_{21}{m}_{32}-m_{22}{m}_{31})\end{array}$$

可以用以下方便记忆

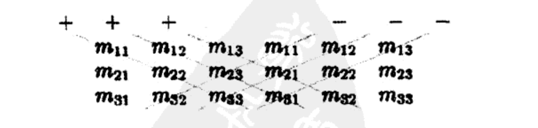
如果将方阵的每个行向量解释为基向量，那么可以简化为

$$\begin{array}{rl}\left|\begin{array}{c}M\end{array}\right|& \\ & =\left|\begin{array}{ccc}{p}_x& p_y& p_z\\ q_x& q_y& q_z\\ r_x& r_y& r_z\end{array}\right|& \\ & =p_x{q}_y{r}_z+p_y{q}_z{r}_x+p_z{q}_x{r}_y-p_z{q}_y{r}_x-p_x{q}_z{r}_y-p_y{q}_x{r}_z\\ & =(p_y{q}_z-p_z{q}_y)r_x+(p_z{q}_x-p_x{q}_z)r_y+(p_x{q}_y-p_y{q}_x)r_z\\ & =(p\times q)·r\end{array}$$

余子式

假设一个矩阵有r行、c列，将M^{ij}表示为删除第i行、第j列得到的矩阵，称这个矩阵为余子式，显然余子式有r-1行、c-1列。

例如一个3x3矩阵：

$$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]$$$$M^{\{12\}}=\left[\begin{array}{cc}4& 6\\ 7& 9\end{array}\right]$$

代数余子式

代数余子式是一个标量，它的值等于对应带符号的余子式的值

$$c_{ij}=(-1{)}^{i+j}\left|\begin{array}{c}{M}^{\{ij\}}\end{array}\right|$$

对于一个三维矩阵而言，符号交错排列：

$$\left[\begin{array}{ccc}+& -& +\\ -& +& -\\ +& -& +\end{array}\right]$$

例如：

$$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]$$$$c_{12}=(-1{)}^3(4\times 9-6\times 7)=-6$$

而且对于任意一个矩阵，取任意行或者任意列，该矩阵的行列式的值等于所取行或列中所有元素与其对应代数余子式的乘积相加的总和

假如对于rxc的矩阵，任取一行i，有：

$$\left|\begin{array}{c}M\end{array}\right|=\sum _{j=1}^c{m}_{ij}{a}_{ij}=\sum _{j=1}^c{m}_{ij}(-1{)}^{i+j}\left|\begin{array}{c}{M}^{\{ij\}}\end{array}\right|$$

例如：

重要性质

• 矩阵积的行列式等于行列式的积

$$\left|\begin{array}{c}AB\end{array}\right|=\left|\begin{array}{c}A\end{array}\right|\left|\begin{array}{c}B\end{array}\right|$$

扩展到n个矩阵相乘：

$$\left|\begin{array}{c}{M}_1{M}_2\cdots M_{n-1}{M}_n\end{array}\right|=\left|\begin{array}{c}{M}_1\end{array}\right|\left|\begin{array}{c}{M}_2\end{array}\right|\cdots \left|\begin{array}{c}{M}_{n-1}\end{array}\right|\left|\begin{array}{c}{M}_n\end{array}\right|$$

• 转置矩阵的行列式与原矩阵的行列式相等

$$\left|\begin{array}{c}{M}^T\end{array}\right|=\left|\begin{array}{c}M\end{array}\right|$$

• 矩阵的任意行或列为0，则该矩阵的行列式也为0
• 交换矩阵的任意两行或两列，该矩阵的行列式符号变为负
• 任意行或列的非零积加到另一行或列上不会改变行列式的值？？？

几何意义

2D

行列式的值等于基向量围成的带符号的平行四边形的面积

3D

行列式的值等于基向量围成的带符号的平行六面体的体积

INFO

行列式的值包含了镜像、投影的信息

• 如果值为0，则包含投影
• 如果值为负数，则包含镜像