圆/球与其他图元

与射线

参考射线与圆/球

与平面

参考平面与圆/球

与AABB

这点和平面与球的相交性测试中计算思想相同

• 计算出球心到AABB上的最近点，并计算出到球心长度
• 比较长度和球心半径

与圆/球

分为两种情况，分别是静态和动态

静态

思想是计算出两个球心之间的距离，比较距离和两球心半径之和的大小，假设两球心距离为d，半径分别是r₁、r₂

• d < r₁、r₂，相交
• d = r₁、r₂，相切
• d > r₁、r₂，不相交

在实践中经常使用平方进行比较，减少了一次取平方根的运算

d² < (r₁ + r₂)²

动态

假设两个球的位移向量分别是d₁、d₂，为了简化讨论，我们将球1认为是“静止的”，两个球体的运动简化为球1相对于球2运动。

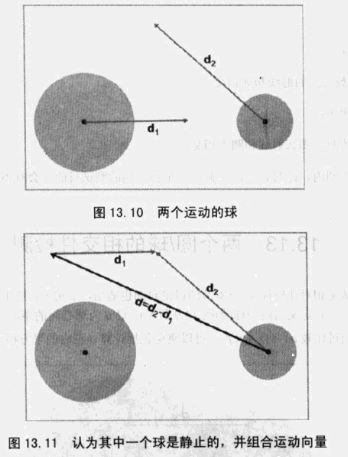
那么球2的位移向量为d = d₂ - d₁，需要将方向向量d标准化，t的取值范围为0到l

运动球的球心为c_m，半径为r_m，那么t时刻，它会运动到c_m + td 位置，目标是计算出相交时刻t

静止球的球心为c_s，半径为r_s

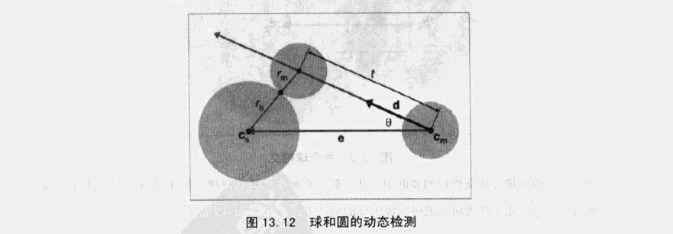
已知以下等式

$$r=r_s+r_m$$$$\mathrm{e}={\mathrm{c}}_s-{\mathrm{c}}_m$$

根据cos定理有

$$r^2=t^2+{\Vert \begin{array}{c}\mathrm{e}\end{array}\Vert }^2-2t\Vert \begin{array}{c}\mathrm{e}\end{array}\Vert \cos \theta$$

简化为

$$t^2-2(\mathrm{e}·\mathrm{d})t+\mathrm{e}·\mathrm{e}-r^2=0$$

根据二次求根公式解得

$$t=\frac{2(\mathrm{e}·\mathrm{d})\pm \sqrt{(-2(\mathrm{e}·\mathrm{d}){)}^2-4(\mathrm{e}·\mathrm{e}-r^2)}}{2}$$

简化后为

$$t=(\mathrm{e}·\mathrm{d})\pm \sqrt{(\mathrm{e}·\mathrm{d}{)}^2-\mathrm{e}·\mathrm{e}+r^2}$$

其中，较小的值是初次接触相交时的t值，较大的值是脱离接触时的t值

• 如果向量e的模长 < r，则球在t=0时刻就相交了
• 如果t < 0或t > l，那么两个球不会相交
• 如果根号下的值为负数，那么两个球不会相交