平面与其他图元

与射线

参考射线与平面

与AABB

静态检测

$img.png$

动态检测

$img.png$

INFO

这里意思没有明白，感觉还是有些模糊

三个平面间的相交性

三个平面相交于一点

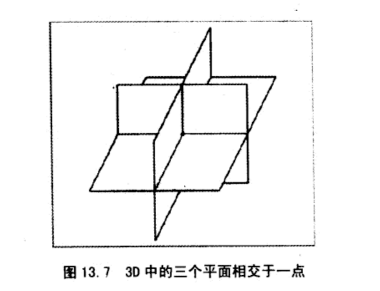
$img.png$

假设三个平面的方程为

p \cdot n_{1} = d_{1}

p \cdot n_{2} = d_{2}

p \cdot n_{3} = d_{3}

联立方程组，计算出交点p的表达式

p = \frac{d_{1} (n_{3} \times n_{2}) + d_{2} (n_{3} \times n_{1}) + d_{3} (n_{1} \times n_{2})}{(n_{1} \times n_{2}) \cdot n_{3}}

当分母为0时，存在任意一对平面平行或重合

与球

静态检测

可以根据球心到平面的距离与球半径的长度比较，判断两者是否相交

球心到平面的距离>球半径，不相交
球心到平面的距离=球半径，相切
球心到平面的距离>球半径，相交

又可以根据交点在正面还是背面，区分为相交在平面正面、平面反面、跨平面

动态检测

假设平面是静止的，球做相对于平面的运动

平面定义为，n为单位向量

p \cdot n = d

球的半径为r，球心位置为向量c，做线性运动，运动方程为c+td，其中d为单位向量指明运动方向

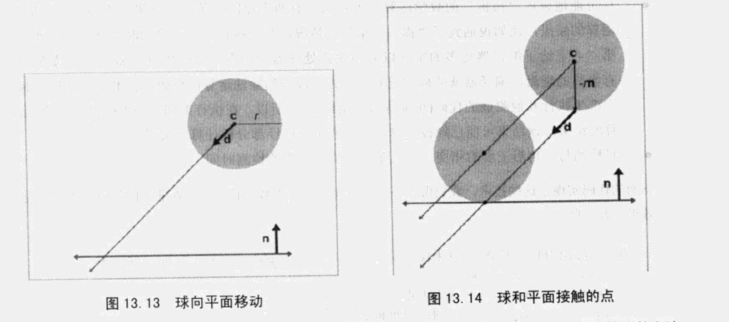
$img.png$

无论与平面上的哪一点相交，在球上的相交点都是固定的。交点处的坐标固定为c - r n。

根据射线与平面的交点坐标公式，将初始点p₀带入

t = \frac{d - (c - r n) \cdot n}{d \cdot n} = \frac{d - c n + r}{d \cdot n}