复数

复数由两部分组成，包含一个实部和一个虚部

$$a+bi$$

其中i满足

$$\sqrt{-1}=i\Rightarrow i^2=-1$$

任意实数都可以用复数表示

$$a+ib,(i=0)$$

因此复数包含实数

$$\mathrm{自}\mathrm{然}\mathrm{数}\subseteq \mathrm{整}\mathrm{数}\subseteq \mathrm{有}\mathrm{理}\mathrm{数}\subseteq \mathrm{实}\mathrm{数}\subseteq \mathrm{复}\mathrm{数}$$

运算规则

• 加法

$$(a+bi)+(c+di)=a+b+(b+d)i$$

• 减法

$$(a+bi)-(c+di)=a-b+(b-d)i$$

• 乘法

$$(a+bi)\times (c+di)=ac+adi+cbi-bd=ac-bd+(ad+cb)i$$

与矩阵的关系

观察上述表达式，可以将结果拆分为矩阵和向量的乘积

$$(a+bi)\times (c+di)=\left[\begin{array}{cc}a& -b\\ b& a\end{array}\right]\left[\begin{array}{c}c\\ d\end{array}\right]=\left[\begin{array}{c}ac-bd\\ bc+ad\end{array}\right]$$

左边为复数的矩阵形式，右边是复数的向量形式

也将其拆分为矩阵形式的乘积

$$(a+bi)\times (c+di)=\left[\begin{array}{cc}a& -b\\ b& a\end{array}\right]\left[\begin{array}{cc}c& -d\\ d& c\end{array}\right]=\left[\begin{array}{cc}ac-bd& -(ad+bc)\\ ad+bc& ac-bd\end{array}\right]$$

接下来我们验证：i²=-1

一个只有实部的特殊复数1+0i的矩阵形式

$$1=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=I$$

可以看出它是一个单位矩阵

一个只有虚部的特殊复数0+i的矩阵形式

$$i=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$$

那么则有

$$i^2=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]=-1$$

共轭复数

"轭"指一同挂载两头牛上的工具，用来一起拉动负载

对于复数而言，只需要将虚部变号就可以得到共轭复数，用p^*表示，例如a+bi的共轭复数为

$$p^{\ast }=a-bi$$

模

计算规则与实数大致相同，复数与共轭复数乘积的平方根的值

$$\Vert \begin{array}{c}p\end{array}\Vert =\sqrt{p{p}^{\ast }}$$$$\Vert \begin{array}{c}x+yi\end{array}\Vert =\sqrt{(x+yi)(x-yi)}=\sqrt{x^2+y^2}$$

在几何上可以将模描述为复数在复平面上的长度

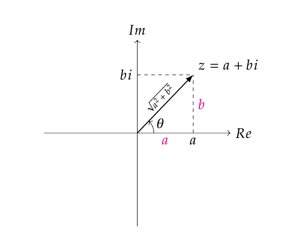
2D平面下的旋转

考虑这样一个2D平面坐标系，实部为x轴，虚部为y轴，则任意一个复数都可以用[x, y]表示

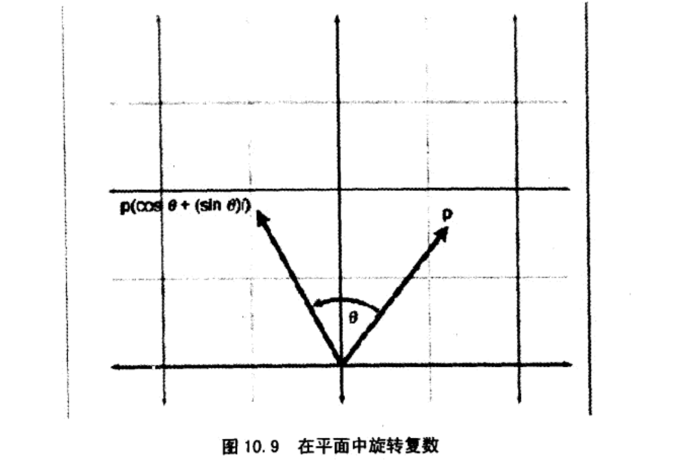
那么旋转角度为θ，我们考虑这样一个复数

$$\cos \theta +i\sin \theta$$

发现满足以下条件

$$(x+yi)(\cos \theta +i\sin \theta )=x\cos \theta -y\sin \theta +(x\sin \theta +y\cos \theta )i$$

这与2x2矩阵产生的效果相同

我们已经知道了复数的向量形式，则有

$$(\left[\begin{array}{cc}x& y\end{array}\right]\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]{)}^T=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}x\cos \theta -y\sin \theta \\ x\sin \theta +y\cos \theta \end{array}\right]$$

旋转的复合

假设有这样一个向量v = x + yi，对它进行两次旋转，角度分别为θ、φ，那么两次旋转可以合并为一次旋转，旋转角度为θ + φ

$$\begin{array}{r}\\ & R(\theta )R(\phi )& \\ & =\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{cc}\cos \phi & \sin \phi \\ -\sin \phi & \cos \phi \end{array}\right]& \\ & =\left[\begin{array}{cc}\cos \theta \cos \phi -\sin \theta \sin \phi & \cos \theta \sin \phi +\sin \theta \cos \phi \\ -(\sin \theta \cos \phi +\cos \theta \sin \phi )& -\sin \theta \sin \phi +\cos \theta \cos \phi \end{array}\right]& \\ & =\left[\begin{array}{cc}\cos (\theta +\phi )& \sin (\theta +\phi )\\ -\sin (\theta +\phi )& \cos (\theta +\phi )\end{array}\right]\end{array}$$

这与旋转角度为θ + φ的转换矩阵相同

也可以通过复数形式的证明

$$\begin{array}{r}\\ & (\cos \theta +i\sin \theta )(\cos \phi +i\sin \phi )\\ & =\cos \theta \cos \phi +i\cos \theta \sin \phi +i\sin \theta \cos \phi -\sin \theta \sin \phi \\ & =\cos \theta \cos \phi -\sin \theta \sin \phi +i(\cos \theta \sin \phi +\sin \theta \cos \phi )\\ & =\cos (\theta +\phi )+i\sin (\theta +\phi )\end{array}$$

参考：

【1】四元数与三维旋转