矩形边界框

用来界定物体的几何框，可以是轴对齐的，也可以是任意方向的。其中轴对齐矩形边框它的边必须是垂直与坐标轴的。

轴对齐矩形边框：axially aligned bounding box（AABB）

方向矩形边界框：oriented bounding box（OBB）

其中AABB是本文讨论的重点

几种包围体的区别：

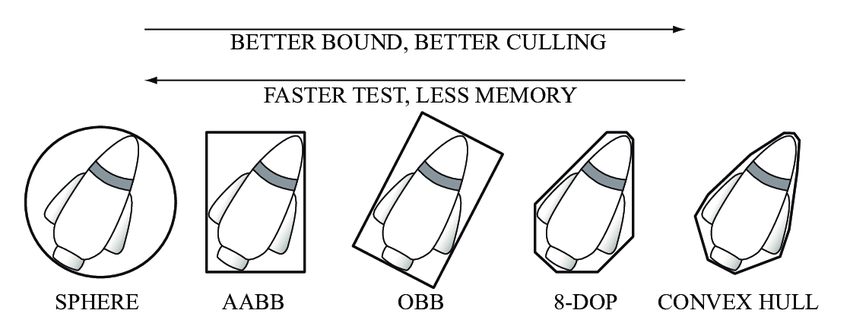
表达方式

边界框中任意一点p(x, y, z)，都满足以下不等式

$$x_{min}\le x\le x_{max}$$$$y_{min}\le y\le y_{max}$$$$z_{min}\le z\le z_{max}$$

特别重要的两个点p_min、p_max

$$p_{min}=\left[\begin{array}{ccc}{x}_{min}& y_{min}& z_{min}\end{array}\right]$$$$p_{max}=\left[\begin{array}{ccc}{x}_{max}& y_{max}& z_{max}\end{array}\right]$$

中心点c为

$$c=\frac{p_{min}+p_{max}}{2}$$

向量s为“尺寸向量”，表示从p_min指向p_max，则有

$$s=p_{max}-p_{min}$$

向量r为“半径向量”，表示从中心点c指向p_max，则有

$$r=p_{max}-c=\frac{s}{2}$$

可知，我们只需要知道边界框的最小点p_min和最大点p_max就可以计算出c、s、r

最小点、最大点计算规则

首先将最小点p_min设置为number类型的最小负值，最大点p_max设置为number类型的最大正值

后遍历构成几何图元的点集，判断出最大值再赋值

AABB与边界球

边界球是将结合图元完全包裹的三维球体，大多数情况下边界球的体积是大于边界框的体积的。在编程上，计算边界框很容易实现，但是计算单位球比较困难

从图中可知，边界框的大小对几何图元的方向很敏感，但是边界球却相反。

变换AABB

物体在虚拟世界中的变换时，我们有两种方式来确定AABB

1. 根据变换后的物体重新计算AABB
2. 随着物体一起变换原有的AABB，这样得到的AABB并不一定是轴对齐的，也不一定是盒装的（如果物体发生了扭曲）

其中第一种方式需要重新遍历整个点集合，比较得出最大值和最小值，效率相对较慢，但是编程实现简单；第二种方式只需要关注边界框的8个点即可，更加简洁、快速，但是编程实现相对复杂

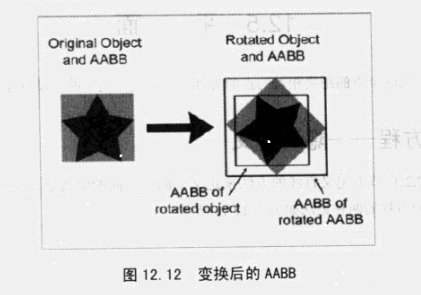
原AABB、变换后的AABB、基于变换后的AABB重新计算出的AABB

变换思路？？