正交投影

一般来说，投影意味着降维。正交是由垂直推广而来，而正交投影是将垂直方向上的缩放因子设置为0，投影后的点与原物体保持平行，因此又称为平行投影。

2D

向坐标轴投影

向x轴投影，则设置y轴方向上的投影因子为0

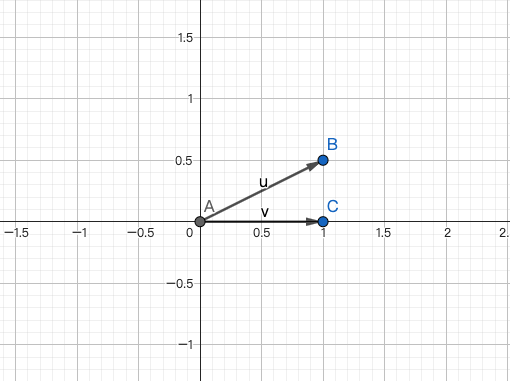
得出转换矩阵为：

$$\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]$$

向y轴投影，则设置x轴方向上的投影因子为0

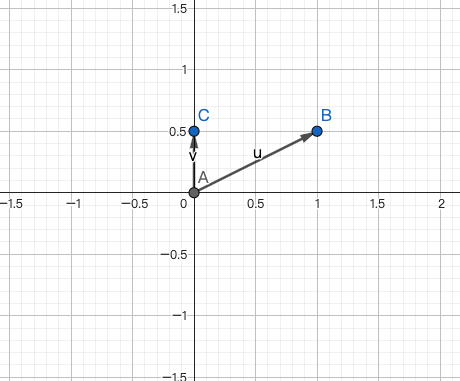
得出转换矩阵为：

$$\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]$$

任意方向的投影

向垂直于单位向量n方向上投影，此时k=0，则得到转换矩阵为：

$$M(n,k)=\left[\begin{array}{c}{p}^{{}^{\prime }}\\ q^{{}^{\prime }}\end{array}\right]=\left[\begin{array}{cc}1-n_x^2& -n_x{n}_y\\ -n_x{n}_y& 1-n_y^2\end{array}\right]$$

3D

向坐标轴投影

向yz平面投影，则设置x轴方向上的投影因子为0

得出转换矩阵为：

$$\left[\begin{array}{ccc}0& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

向xz平面投影，则设置y轴方向上的投影因子为0

得出转换矩阵为：

$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right]$$

向xy平面投影，则设置z轴方向上的投影因子为0

得出转换矩阵为：

$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]$$

任意平面投影

向垂直于单位向量n的平面投影

$$M(n,k)=\left[\begin{array}{c}{p}^{{}^{\prime }}\\ q^{{}^{\prime }}\\ r^{{}^{\prime }}\end{array}\right]=\left[\begin{array}{ccc}1-n_x^2& -n_x{n}_y& -n_x{n}_z\\ -n_x{n}_y& 1-n_y^2& -n_y{n}_z\\ -n_x{n}_z& -n_z{n}_y& 1-n_z^2\end{array}\right]$$