放缩

根据比例因子k控制对物体的缩放，如果每个方向上的缩放因子相同，则为均匀缩放，反之则为非均匀缩放。

均匀缩放时，在二维坐标系中，面积增大k²；在三维坐标系中，体积增大k³

• 缩放因子k < 0时为镜像
• 缩放因子k = 0时为正交投影
• 缩放因子k > 0时为普通缩放，而且0 < k < 1时为缩小，k > 1时为放大，本文主要讨论k > 0的情况。

2D

最简单的缩放是沿着坐标轴进行放大、缩小，假设x轴方向的缩放因子为k_x，y轴方向的缩放因子为k_y

则

$$M=\left[\begin{array}{c}{p}^{{}^{\prime }}\\ q^{{}^{\prime }}\end{array}\right]=\left[\begin{array}{cc}{k}_x& 0\\ 0& k_y\end{array}\right]$$

任意轴缩放

给定向量v沿着单位向量n放缩，放缩因子为k，使用n、v、k表示缩放后的向量v^'

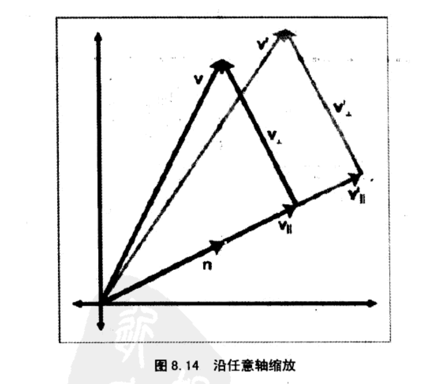
将向量v拆分为沿向量n的水平分量v_∥和垂直分量v_⊥，将向量v^'也拆分为沿向量n的水平分量v_∥^'和垂直分量v_⊥^'

由于v_⊥^'垂直与缩放轴，所以它不受缩放因子的影响。

根据以上信息可知：

$$\begin{array}{rl}{v}^{{}^{\prime }}& \\ & =v_{\parallel }^{{}^{\prime }}+v_{\perp }^{{}^{\prime }}\\ & =v_{\parallel }^{{}^{\prime }}+v_{\perp }\\ & =k(v·n)n+v-v_{\parallel }\\ & =k(v·n)n+v-(v·n)n\\ & =(k-1)(v·n)n+v\end{array}$$

带入对应坐标轴的基向量可知

x轴方向

$$p=\left[\begin{array}{cc}1& 0\end{array}\right]$$$$\begin{array}{r}{p}^{{}^{\prime }}\\ & =(k-1)(p·n)n+p\\ & =(k-1)(\left[\begin{array}{c}1\\ 0\end{array}\right]·\left[\begin{array}{c}{n}_x\\ n_y\end{array}\right])\left[\begin{array}{c}{n}_x\\ n_y\end{array}\right]+\left[\begin{array}{c}1\\ 0\end{array}\right]\\ & =\left[\begin{array}{c}1+(k-1)n_x^2\\ (k-1)n_x{n}_y\end{array}\right]\end{array}$$

y轴方向

$$q=\left[\begin{array}{cc}0& 1\end{array}\right]$$$$q^{{}^{\prime }}=\left[\begin{array}{c}(k-1)n_x{n}_y\\ 1+(k-1)n_y^2\end{array}\right]$$

得出转换矩阵为：

$$M(n,k)=\left[\begin{array}{c}{p}^{{}^{\prime }}\\ q^{{}^{\prime }}\end{array}\right]=\left[\begin{array}{cc}1+(k-1)n_x^2& (k-1)n_x{n}_y\\ (k-1)n_x{n}_y& 1+(k-1)n_y^2\end{array}\right]$$

3D

在3D中，如果也是沿着坐标轴缩放，那么转换矩阵为：

$$M=\left[\begin{array}{c}{p}^{{}^{\prime }}\\ q^{{}^{\prime }}\\ r^{{}^{\prime }}\end{array}\right]=\left[\begin{array}{ccc}{k}_x& 0& 0\\ 0& k_y& 0\\ 0& 0& k_z\end{array}\right]$$

任意平面缩放

同样的将各个坐标轴上的基向量带入上述表达式中，可知3D下的转换矩阵为：

$$M(n,k)=\left[\begin{array}{c}{p}^{{}^{\prime }}\\ q^{{}^{\prime }}\\ r^{{}^{\prime }}\end{array}\right]=\left[\begin{array}{ccc}1+(k-1)n_x^2& (k-1)n_x{n}_y& (k-1)n_x{n}_z\\ (k-1)n_x{n}_y& 1+(k-1)n_y^2& (k-1)n_y{n}_z\\ (k-1)n_x{n}_z& (k-1)n_z{n}_y& 1+(k-1)n_z^2\end{array}\right]$$