旋转
这里我们先不考虑平移,而且进一步限制物体只围绕着原点旋转,旋转角度为θ
2D
经常认为逆时针是正方向,顺时针是反方向
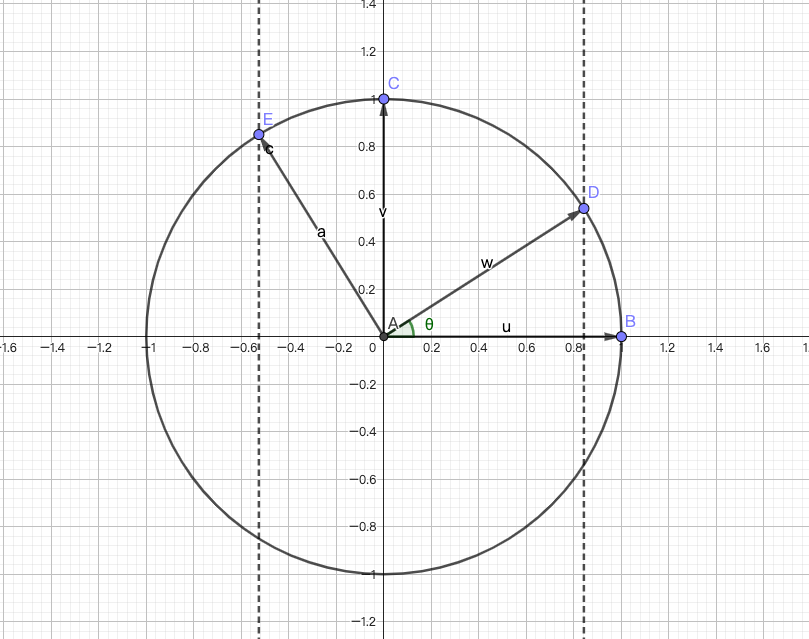
对应的转换矩阵为:
3D
在左手坐标系、右手坐标系中,而且根据所处的位置不同看到的正方向也是不同的
例如在左手坐标系中判断正方向时,左手大拇指方向朝向对应轴的正端点,四指弯曲的方向为旋转的正方向。
从哪里看也会影响正方向的判断,一般认为是从原点看向对应端点,对应表格中的从轴的负端点向正端点看。
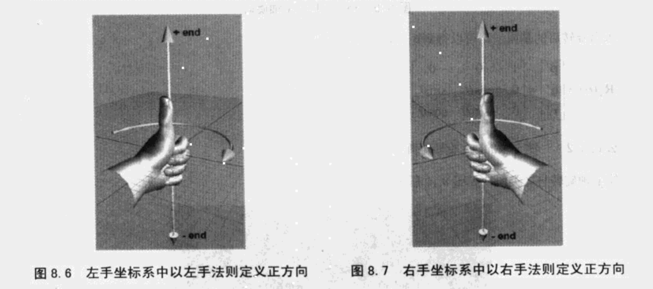
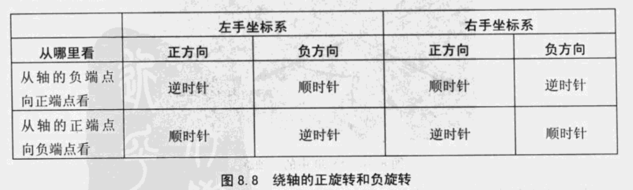
绕坐标轴旋转
绕x轴旋转
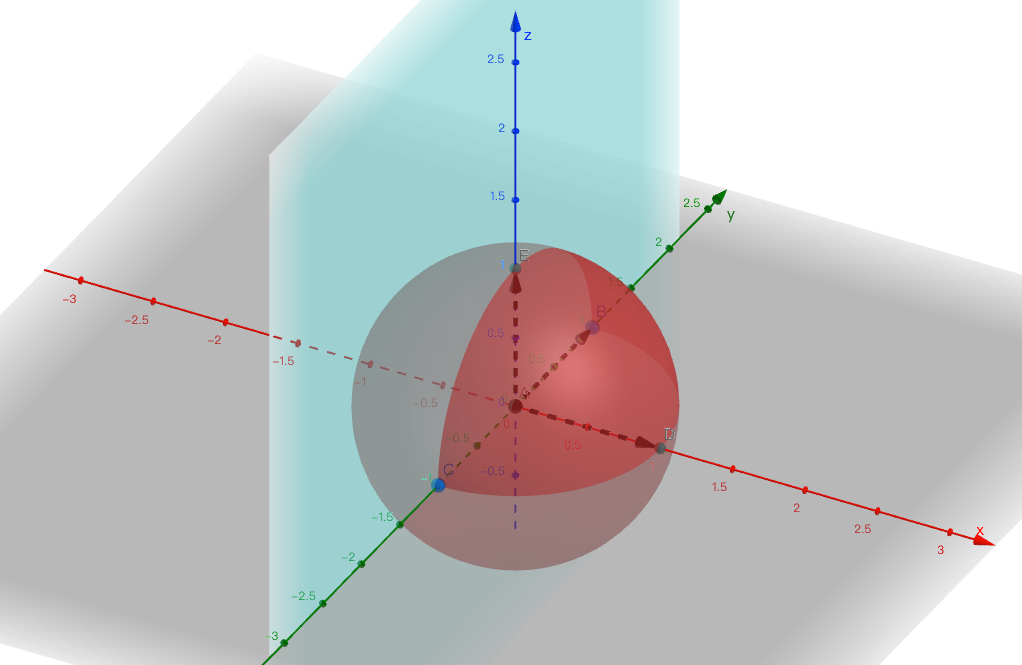
去掉球体,简化后的图形
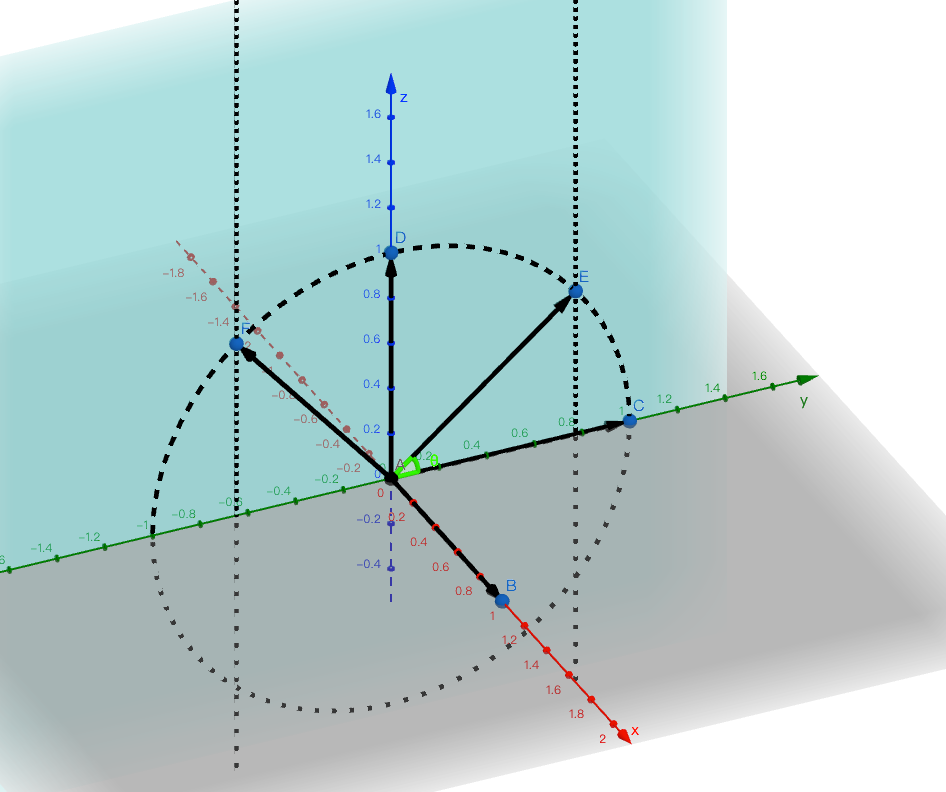
可以得出转换矩阵为:
绕y轴旋转
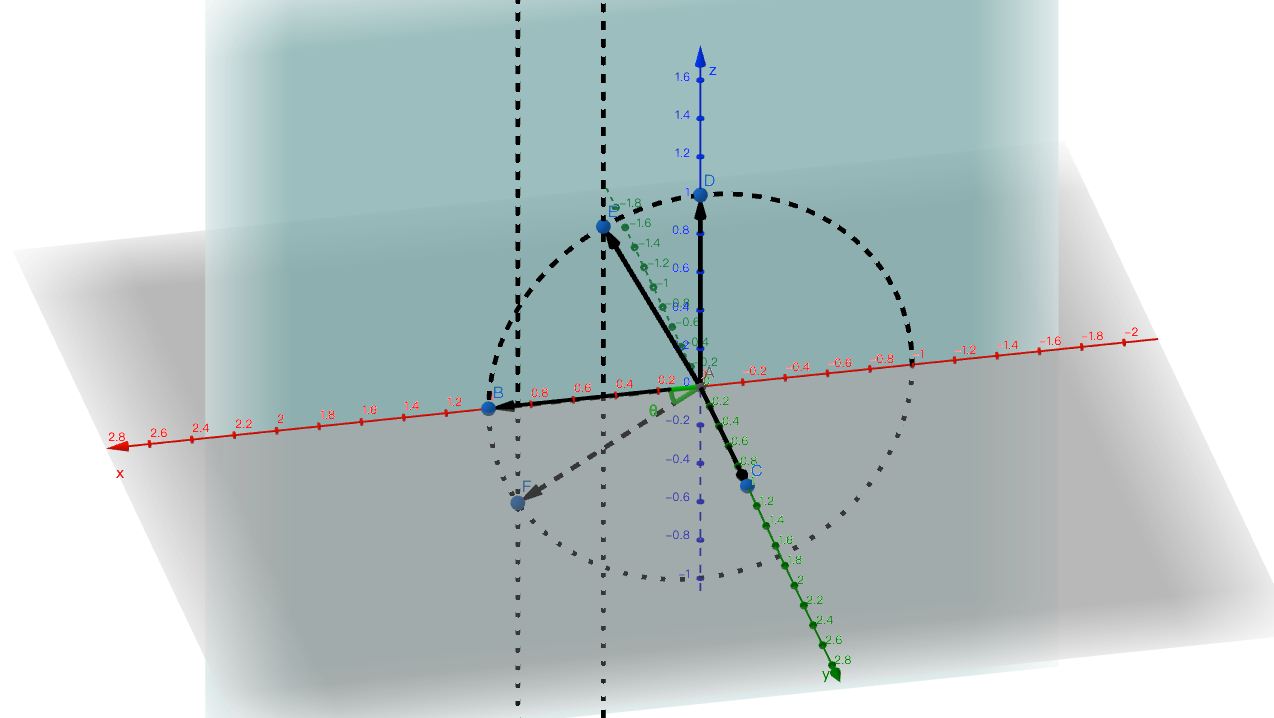
可以得出转换矩阵为:
绕z轴旋转
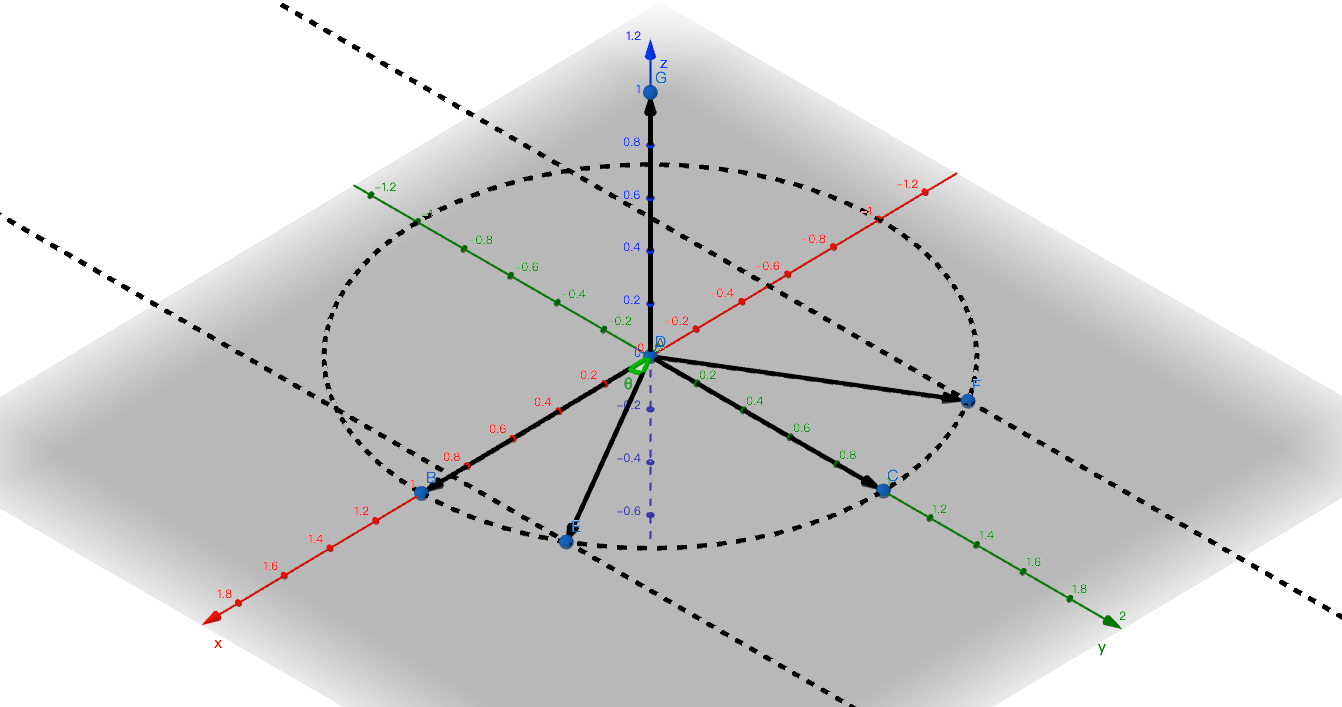
可以得出转换矩阵为:
绕任意轴旋转
在三维中,向量绕任意轴旋转情况更复杂,但是也更少见。这里我们依旧不考虑平移,假设旋转轴通过原点。
假设旋转轴为n且为单位向量,旋转角度为θ,需要旋转的向量是v,我们要计算出满足以下条件的矩阵:
用n、r、θ表示转换后的向量
推导过程如下:

将向量v拆分为水平方向上的向量:
垂直方向上的向量:
而且
对应的旋转后的向量也满足:
而且旋转时,旋转后向量水平方向上的分量与原向量水平方向的分量相等
所以我们只需要计算出v⊥'即可计算出旋转后向量v'
原向量v的水平分量和旋转轴n构成一个平面,并且向量w为该平面的法向量,根据叉乘的几何意义可知:
而且向量w的长度等于向量n和向量v⊥构成的平行四边形面积,而且向量n与向量v⊥相垂直,所以围成的多边形是矩形。又因为向量n为单位向量,长度固定为1,所以向量w的长度等于向量v⊥的长度
旋转后的向量的垂直分量可以表示为:
将已知的信息带入上述公式可知:
将三维坐标轴的基向量分别带入上述表表达式
将x轴的基向量带入可知
相应的计算出q'、r'
最终得到的矩阵为:
INFO
为什么这个等式是成立的呢?
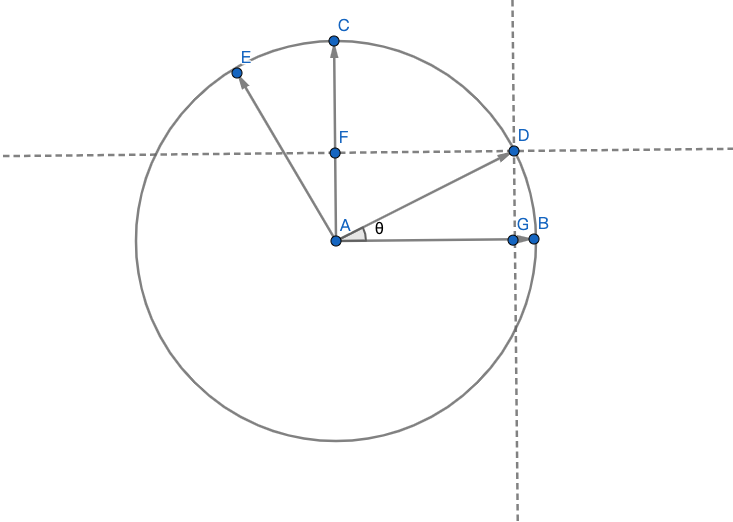
已知
推导过程如下:

