欧拉角

欧拉角能描述任意旋转，也就是说任意旋转都可以按照顺序，做三个欧拉角的旋转而得到。

欧拉角的基本思想是将绕三个相互垂直的轴做三次旋转，下次的旋转总是与上次旋转后的轴有关，这样保证了旋转之间的联系，联想嵌套坐标系

这也是为什么第一次旋转时是绕世界坐标系的轴

要指出，我们平时说的欧拉角其实还可以细分为经典欧拉角(Euler-angles)和泰特布莱恩角(Tait-Bryan-angles)，这两种方法都利用了笛卡尔坐标系的三轴作为旋转轴，主要区别在于选取顺序。

欧拉角又可以根据物体坐标轴是否静止分为静态和动态：

• 静态： 即绕世界坐标系三个轴的旋转，由于物体旋转过程中坐标轴保持静止，所以称为静态，此时各个变换顺序的旋转矩阵是左乘的

• 动态： 即绕物体坐标系三个轴的旋转，由于物体旋转过程中坐标轴随着物体做相同的转动，所以称为动态，此时各个变换顺序的旋转矩阵是右乘的

欧拉角选取顺序有以下6种

$$(x,y,x)$$$$(x,z,x)$$$$(y,x,y)$$$$(y,z,y)$$$$(z,x,z)$$$$(z,y,z)$$

可以简化了理解为绕a轴旋转，再绕旋转一次后的b轴旋转，再绕旋转两次后的a轴旋转

泰特布莱恩角选取顺序有以下6种

$$(x,y,z)$$$$(x,z,y)$$$$(y,x,z)$$$$(y,z,x)$$$$(z,x,y)$$$$(z,y,x)$$

泰特-布莱恩角（Tait–Bryan angles）又常称为：roll-偏航角、pitch-俯仰角、yaw-翻滚角

WARNING

heading-pitch-bank系统等价于roll-pitch-yaw系统，注意两者的排列顺序，roll类似bank，yaw类似heading

例如：heading20度，pitch30度，bank40度 等价于 yaw20度，pitch30度，roll40度

heading-pitch-bank思想是让物体开始于标准"方位"--物体坐标系与惯性坐标系坐标轴对齐，在标准方位上进行heading、pitch、bank以达到我们期望的方位

本文以经典欧拉角(Euler-angles)以[z,x,z]顺序旋转

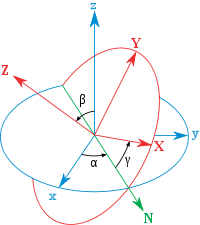
图中有两组坐标：

• [x, y, z]为全局坐标，保持不动
• [X, Y, Z]为局部坐标，随着物体移动

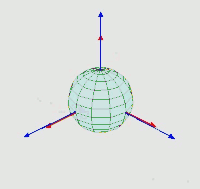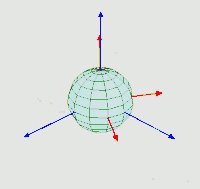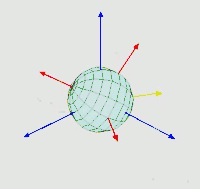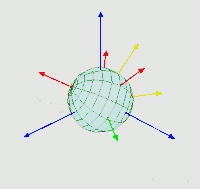
我们取α、β、γ三个角，分别代表

• α为x轴与旋转一次后的x轴的夹角，即为绕z轴旋转的角度
• β为旋转一次后的x轴与旋转三次后的x轴的夹角，即为绕x轴旋转的角度
• γ为z轴与旋转一次后的z轴的夹角，即为绕z轴旋转的角度

得到[z,x,z]顺序下的组合矩阵为

$$\begin{array}{rl}M& \\ & =\left[\begin{array}{ccc}\cos \alpha & \sin \alpha & 0\\ -\sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \beta & \sin \beta \\ 0& -\sin \beta & \cos \beta \end{array}\right]\left[\begin{array}{ccc}\cos \gamma & \sin \gamma & 0\\ -\sin \gamma & \cos \gamma & 0\\ 0& 0& 1\end{array}\right]\\ & =\left[\begin{array}{ccc}\cos \alpha \cos \gamma -\sin \alpha \cos \beta \sin \gamma & -\sin \alpha \cos \gamma -\cos \alpha \cos \beta \sin \gamma & \sin \beta \sin \gamma \\ \cos \alpha \sin \gamma +\sin \alpha \cos \beta \cos \gamma & -\sin \alpha \sin \gamma +\cos \alpha \cos \beta \cos \gamma & -\sin \beta \cos \gamma \\ \sin \alpha \sin \beta & \cos \alpha \sin \beta & \cos \beta \end{array}\right]\end{array}$$

INFO

• 任意三个轴都可以作为旋转轴，不一定是笛卡尔坐标轴，但是笛卡尔坐标轴更有意义
• 旋转可以以任意顺序进行，最终都会得到相同的效果
• 我们只需要知道三个旋转角度便可以对物体进行旋转

优点

• 占用空间小，只需要知道三个角度便可以进行旋转
• 更简单，更符合人类的思维，通过旋转角度更加具象的描述了旋转
• 表达方式简洁
• 任意三个欧拉角度都是有意义的

缺点

• 有歧义的，给定方位的表述不唯一，会存在多个欧拉角对应一个方位，又称为别名现象

经典欧拉角(Euler-angles)，顺序为[z,x,z]示例

泰特布莱恩角(Tait-Bryan-angles)，顺序为[z,x,y]示例

别名问题

由于一个旋转对应多个欧拉角，考虑以下两个问题

1. 将一个角度加上360度的倍数，尽管数值改变了，但是方位并没有改变，这是最简单的别名问题

解决上述问题，我们只需要对欧拉角的数值进行限制即可

$$heading\in \left[\begin{array}{cc}-{180}^{°}& {180}^{°}\end{array}\right],bank\in \left[\begin{array}{cc}-{180}^{°}& {180}^{°}\end{array}\right],pitch\in \left[\begin{array}{cc}-{90}^{°}& {90}^{°}\end{array}\right]$$

如果patch等于90度或-90度，则bank为0

2. 三个角度不相互独立，任意一个角度都可以通过另外一个欧拉角变换而来

例如：pitch135度等价于heading180度，pitch45度，bank180度

欧拉角最著名的别名问题是：先heading45度，再pitch90度与先pitch90度，再yaw45度的结果是相同的

更一般来说，在进行旋转时，只要欧拉角中间的旋转角度为

$$\pm {90}^{°}$$

便会存在第一次旋转与第三次旋转绕相同的轴，则会丢失一个维度，只能绕竖直轴旋转。这种现象又称为万向锁。

旋转过程中万向锁问题时，会出现旋转不自然、抖动、突然飘起来像是"挂"起来一样

添加范围限制能解决部分别名问题，但是无法解决万向锁问题，万向锁问题可以通过选择合理的旋转顺序或者四元数解决

总结

• 欧拉角使用三个旋转量保存方位，占用空间更少
• 在多数情况下，欧拉角更加易于使用
• 任意3个角度构成的欧拉角都有意义
• 欧拉角存在别名问题，这与角度的周期性和旋转的不独立性有关
• 限制欧拉角值的范围可以解决许多基本问题
• 如果patch等于正负90度时，会导致万向锁问题，可以通过选择合理的旋转顺序或者四元数解决

参考：

【1】欧拉角

【2】环架锁定

【3】欧拉角

【4】马同学图解数学