平面

在3D中，到任意两点距离相等的点的集合为平面

隐式定义

像在2D中定义直线那样，在3D中定义平面为

a x + b y + c z = d

相应的向量方式为

p \cdot n = d

其中p为平面上的任意点，向量n为p所在平面的法向量

假设p、q都在平面上，则有

q \cdot n = d

p \cdot n - q \cdot n = 0 \Rightarrow (p - q) \cdot n = 0

根据点乘的几何意义何止，向量n垂直与p到q向量所在的平面，为了简化计算，我们一般将向量n认为是单位向量

已知平面上三个点，p₁、p₂、p₃，根据上文可知向量n是垂直于3点确定的平面的，那么根据叉乘的几何意义可知

n = \frac{(p_{2} - p_{1}) \times (p_{3} - p_{2})}{‖ \begin{matrix} (p_{2} - p_{1}) \times (p_{3} - p_{2}) \end{matrix} ‖}

计算出单位向量n后，任意选择一个点带入上述隐式定义公式即可计算出d值，从而确定唯一的平面表达式。

多于三个点的点集，并不一定都在同一个平面上，也有可能平面是弯曲的，那么如何计算出点集对应的最佳平面呢？

\begin{aligned} p_{1} = [\begin{array}{c} x_{1} & y_{1} & z_{1} \end{array}] \\ p_{2} = [\begin{array}{c} x_{2} & y_{2} & z_{2} \end{array}] \\ ⋮ \\ p_{n - 1} = [\begin{array}{c} x_{n - 1} & y_{n - 1} & z_{n - 1} \end{array}] \\ p_{n} = [\begin{array}{c} x_{n} & y_{n} & z_{n} \end{array}] \end{aligned}

则向量n的最佳坐标为

\begin{aligned} n_{x} \\ = (z_{1} + z_{2}) (y_{1} - y_{2}) + (z_{2} + z_{3}) (y_{2} - y_{3}) + \\ \dots \\ + (z_{n - 1} + z_{n}) (y_{n - 1} - y_{n}) + (z_{n} + z_{1}) (y_{n} - y_{1}) \\ = \sum_{i = 1}^{n - 1} (z_{i} + z_{i + 1}) (y_{i} - y_{i + 1}) \end{aligned}

\begin{aligned} n_{y} \\ = (x_{1} + x_{2}) (z_{1} - z_{2}) + (x_{2} + x_{3}) (z_{2} - z_{3}) + \\ \dots \\ + (x_{n - 1} + x_{n}) (z_{n - 1} - z_{n}) + (x_{n} + x_{1}) (z_{n} - z_{1}) \\ = \sum_{i = 1}^{n - 1} (x_{i} + x_{i + 1}) (z_{i} - z_{i + 1}) \end{aligned}

\begin{aligned} n_{z} \\ = (y_{1} + y_{2}) (x_{1} - x_{2}) + (y_{2} + y_{3}) (x_{2} - x_{3}) + \\ \dots \\ + (y_{n - 1} + y_{n}) (x_{n - 1} - x_{n}) + (y_{n} + y_{1}) (x_{n} - x_{1}) \\ = \sum_{i = 1}^{n - 1} (y_{i} + y_{i + 1}) (x_{i} - x_{i + 1}) \end{aligned}

根据计算出的向量n的坐标，再计算d值

d = \frac{1}{n} \sum_{i = 1}^{n} p_{i} \cdot n = \frac{1}{n} (\sum_{i = 1}^{n} p_{i}) n

INFO

主要点的顺序需要按照多边形顺时针排列，否则计算出的单位向量n方向是相反的

任意点到平面的最短距离，也就是垂直与平面的距离，假设任意点为q，向量p为平面上一点而且与q之间的距离是最短距离，则有q到p的向量垂直于平面

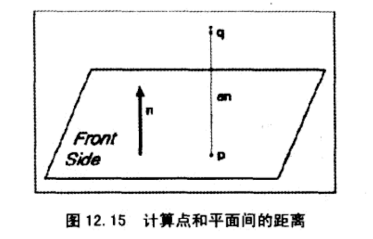
$img.png$

根据向量加法，有

p + a \cdot n = q \Rightarrow (p + a \cdot n) \cdot n = q \cdot n \Rightarrow d + a = q \cdot n \Rightarrow a = q \cdot n - d