变换的组合

将多个矩阵组合按照顺序连接在一起构成一个新的矩阵，表示多个变换的组合

例如物体从物体坐标系转换到世界坐标系，再转换到摄像机坐标系，转换的过程本质是物体上点的转换，有以下转化过程：

$${\mathrm{P}}_{\mathrm{世}\mathrm{界}}={\mathrm{P}}_{\mathrm{物}\mathrm{体}}{\mathrm{M}}_{\mathrm{物}\mathrm{体}⟶\mathrm{世}\mathrm{界}}$$$${\mathrm{P}}_{\mathrm{摄}\mathrm{像}\mathrm{机}}={\mathrm{P}}_{\mathrm{世}\mathrm{界}}{\mathrm{M}}_{\mathrm{世}\mathrm{界}⟶\mathrm{摄}\mathrm{像}\mathrm{机}}=({\mathrm{P}}_{\mathrm{物}\mathrm{体}}{\mathrm{M}}_{\mathrm{物}\mathrm{体}⟶\mathrm{世}\mathrm{界}}){\mathrm{M}}_{\mathrm{世}\mathrm{界}⟶\mathrm{摄}\mathrm{像}\mathrm{机}}={\mathrm{P}}_{\mathrm{物}\mathrm{体}}{\mathrm{M}}_{\mathrm{物}\mathrm{体}⟶\mathrm{摄}\mathrm{像}\mathrm{机}}$$

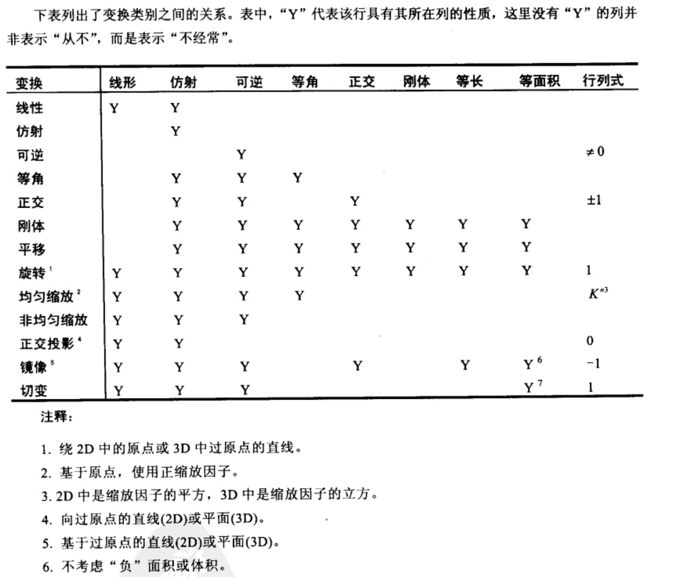
变换的分类

我们根据变换的性质进行分类，可以将一般意义上的转换认为是映射或函数，其实本质是一定规则的运算，根据输入计算出输出。

线性变换

我们认为如果满足以下条件，则称为线性变换：

$$f(\mathrm{a}+\mathrm{b})=f(\mathrm{a})+f(\mathrm{b})$$$$f(k\mathrm{a})=kf(\mathrm{a})$$

可以理解对向量空间中任意一个向量的进行变换的效果可以分解为对两个分向量进行变换后的向量之和

比较重要的两个引理：

1. 如果F(a)=aM，其中M为任意方阵，那么则称F(a)为线性变换。证明如下：

$$f(\mathrm{a}+\mathrm{b})=(\mathrm{a}+\mathrm{b})\mathrm{M}=\mathrm{a}\mathrm{M}+\mathrm{b}\mathrm{M}=f(\mathrm{a})+f(\mathrm{b})$$$$f(k\mathrm{a})=k\mathrm{a}\mathrm{M}=k(\mathrm{a}\mathrm{M})=kf(\mathrm{a})$$

2. 零向量的任意线性变化还是零向量

INFO

在某些文献中，将线性变换定义为对于一个平行线来说，如果变换之后仍是平行线，那么称这个变换为线性变换。

但是以上表述有一个缺陷，对于投影而言，一条线投影之后可能是一个点，这也无谓'平行'

旋转、放缩、正交投影、镜像、切变都是线性变换。

INFO

证明放缩是线性变换

假设3D量空间中有向量u、向量v，沿着坐标轴进行放缩，放缩因子分别是k_x，k_y，k_z

那么对向量u、向量v分别进行放缩，则

$$f(\mathrm{u})=k_x{\mathrm{u}}_x+k_y{\mathrm{u}}_y+k_z{\mathrm{u}}_z$$$$f(\mathrm{v})=k_x{\mathrm{v}}_x+k_y{\mathrm{v}}_y+k_z{\mathrm{v}}_z$$

将两者相加可知

$$\begin{array}{r}\\ & f(\mathrm{u})+f(\mathrm{v})& \\ & =k_x{\mathrm{u}}_x+k_y{\mathrm{u}}_y+k_z{\mathrm{u}}_z+k_x{\mathrm{v}}_x+k_y{\mathrm{v}}_y+k_z{\mathrm{v}}_z\\ & =k_x({\mathrm{u}}_x+{\mathrm{v}}_x)+k_y({\mathrm{u}}_y+{\mathrm{v}}_y)+k_z({\mathrm{u}}_z+{\mathrm{v}}_z)\\ & =f(\mathrm{u}+\mathrm{v})\end{array}$$

任意一个标量s相乘，有

$$f(s\mathrm{u})=s{k}_x{\mathrm{u}}_x+s{k}_y{\mathrm{u}}_y+s{k}_z{\mathrm{u}}_z=s(k_x{\mathrm{u}}_x+k_y{\mathrm{u}}_y+k_z{\mathrm{u}}_z)=sf(\mathrm{u})$$

因此可知放缩是线性变换

仿射变换

仿射变换是线性变换的超集，线性变换一定是仿射变换，仿射变换不一定是线性变换。

因此我们讨论的旋转、放缩、正交投影、镜像、切变都是仿射变换。

任何具有以下形式的变换都是仿射变换。

$${\mathrm{v}}^{{}^{\prime }}=\mathrm{v}\mathrm{M}+b$$

可逆变换

如果一个变换后的结果可以撤销还原成原坐标，那么这个变换是可逆的。旋转、放缩、镜像、切变都是可逆的，但是投影是不可逆的，因为投影本质是降维，导致原维度的信息丢失而无法可逆。

从代数上来说，判断一个转换矩阵是否为可逆变换，如果转换矩阵存在逆矩阵，那么我们称该转换矩阵是可逆的。

等角变换

如果变换前后两个向量的夹角、方向不变，那么我们称该变换为等角变换。其中旋转、均匀放缩、旋转是等角变换。

所有的等角变换都是仿射变换和可逆的。

正交变换

如果变换前后，体积、面积、角度、长度都保持不变，那么这个变换为正交变换。正交变换的基本思想是保持垂直，且不进行缩放变换。

平移、旋转和镜像是仅有的正交变换，所有的正交变换都是仿射变换和可逆的。

刚体变换

如果变换只改变了物体的位置和方向，并没有改变长度、大小、体积、面积，那么这个变换为刚体变换。

平移和旋转是仅有的刚体变换，镜像并不被认为是刚体转换，所有的刚体变换都是仿射变换、可逆的、正交的、等角。

总结