多边形

对于多边形并没有一个准确的定义，一般来说，多边形是由顶点和边构成的平面物体

简单多边形和复杂多边形

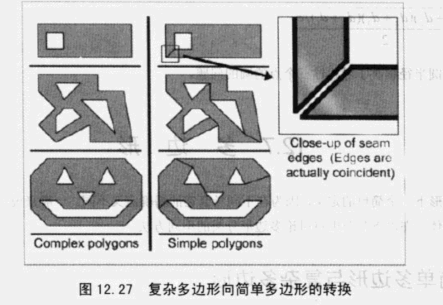
简单多边形是不包含“洞”的，反之复杂多边形是包含的。

但是复杂多边形可以通过分割转换为简单多边形

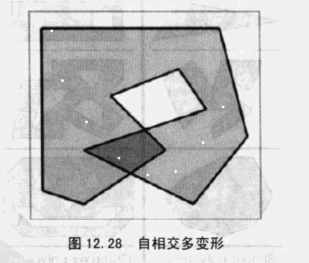
自相交多边形

大多数简单多边形是不与自己相交的，而且我们并不经常与自相交多边形打交道

凸多边形和凹多边形

非自相交多边形又可以分为凸多边形和凹多边形，但是由于存在退化四边形，对于凹凸并没有准确的定义，但是我们给出以下常见定义：

• 直观上，凸多边形是没有任何“凹陷点”的，凹多边形是至少有一个“凹陷点”
• 凸多边形任意两点的连线都是在四边形内部，凹多边形至少存在两个点的连线其中一部分是在四边形外部的
• 沿多边形周边移动时，凸多边形的方向转向总是一致的，凹多边形方向并不是一致的（假设你是小汽车的驾驶员，沿着周边移动），但是这只针对非自相交多边形

而且为了减少凹凸多边形退化导致的检查模糊问题，我们约定

• 只对凸多边形有效的代码，对于这个多边形也有效，那么这个多边形是凸多边形
• 如果凸多边形测试的代码中检查到这个多边形是凸多边形，那么它就是凸多边形

凹凸检查

根据给出的凹凸多边形的定义，有三种方式

凹陷点

判断多边形是否有凹陷点，有则为凹多边形，反之为凸多边形

转向

向量的点乘可以计算某两个边构成的法向量，并根据

• 凸四边形中所有点的法向量与凸四边形所在平面的法向量的点乘是正直，即方向相同
• 凸四边形为负值，即方向不同

内角和

对于任意一个n多边形，它有n个顶点，那么通过顶点之间的连线可以切割成n-2个三角形，则这个n多边形的内角和为(n-2)*180

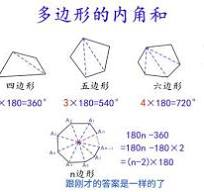
但是凸多边形和凹多边形的内角和都是(n-2)*180，为了解决这个问题，我们取每个顶点最小的角（包含图中标出的两个角）

• 凸多边形：每个顶点最小的角之和是(n-2)*180
• 凸多边形：每个顶点最小的角之和小于(n-2)*180

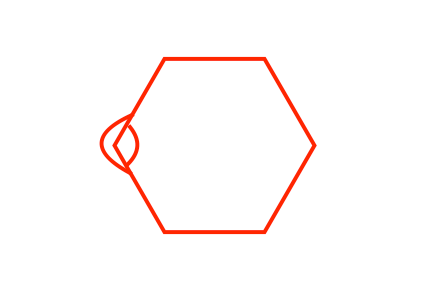
而点乘可以计算出两个向量的夹角，从而判断出最小的弧度值

import { Vector3 } from './Vector3';
import { kPi, safeAcos } from './MathUtil';

/**
 * 多边形凹凸性判断
 *
 * @param v1 多边形点集合
 */
export function isConvex(v1: Vector3[]) {
  // 最小角度值之和
  let angleSum = 0;

  const n = v1.length;
  for (let i = 0; i < n; i++) {
    // 注意第一个和最后一个点的计算规则

    let e1: Vector3;
    if (i === 0) {
      e1 = v1[n - 1].subtract(v1[i]);
    } else {
      e1 = v1[i - 1].subtract(v1[i]);
    }

    let e2: Vector3;
    if (i === n - 1) {
      e2 = v1[0].subtract(v1[i]);
    } else {
      e2 = v1[i + 1].subtract(v1[i]);
    }

    e1.normalize();
    e2.normalize();

    const dot = e1.multiply(e2) as number;

    const theta = safeAcos(dot);
    angleSum += theta;
  }

  // 计算内角和
  const convexAngleSum = (n - 2) * kPi;
  // 判断凹凸性，并允许一部分精度误差
  return angleSum >= convexAngleSum - n * 0.0001;
}

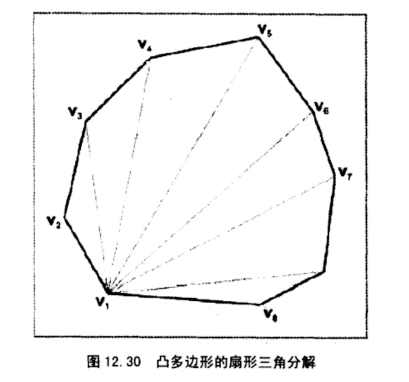
三角分解和扇形分解

任意多边形都可以分解成多个三角形，但是对于复杂、自相交甚至简单多边形都不是一件容易的事情。

为了方便起见，我们任意选择一个简单多边形，并在多边形中任选一个顶点作为起点，连接其他顶点将多边形切分成多个“细长”的三角形

INFO

1. 什么是退化？

在定义限制下，属于一个集合中的对象由于性质改变而变成另外一个集合的对象，一般情况是变成简单集合的对象

例如：

点是退化的圆，因为一个圆若半径为0就会成一个点

圆是退化的椭圆，因为它的离心率是0

线是退化的抛物线，因为抛物线在切空间中呈一直线

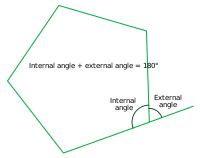
2. 什么是内角、外角、补角？

内角：多边形内部的角

外角：多边形内角邻边延长线构成的角

补角：形容一种角之间的关系，互为补角，简称为互补角，内角+外角=180

参考：

【1】退化多边形

【2】退化