四元数

那么如何将复数从2D扩展到3D中呢，答案是引入三个虚部，分别用i、j、k表示，并且满足

$$\begin{array}{r}\\ & i^2=j^2=k^2=ijk=-1\end{array}$$

进而可知

放到表格中有

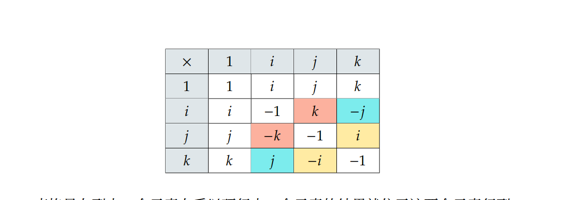
那么一个四元数定义了3D中的复数

$$w+xi+yj+zk$$

可以记作

$$[w,x,y,z]$$

也可以简化记作

$$[w,v]$$

同样的，3D中的复数（即四元数）也满足2D中复数的运算规则，而且也支持旋转3D向量旋转

负四元数

将实部和虚部都取复数即可

$$-q=\left[\begin{array}{cc}-w& -v\end{array}\right]=\left[\begin{array}{cccc}-w& -x& -y& -z\end{array}\right]$$

3D中任意角位移都有两个不同的四元数表示，而且它们互相为负

加法和减法

四元数的加减法与复数计算规则相同，只需要将对应位置的值相加减即可

例如加法：

$$\begin{array}{r}\\ & q_1+q_1& \\ & =w_1+x_{1}i+y_{1}j+z_{1}k+(w_2+x_{2}i+y_{2}j+z_{2}k)\\ & =w_1+w_2+(x_1+x_2)i+(y_1+y_2)j+(z_1+z_2)k\end{array}$$

简化为

$$q_1+q_1=[w_1+w_2,v_1+v_2]$$

单位四元数

如果一个四元数的虚部都为0，那么称这个四元数为单位四元数

$$q=1+0x+0y+0z=1$$

同样的，任意四元数乘以单位四元数，结果仍是原四元数

共轭和逆

按照共轭复数的形式，定义四元数的共轭时同样将虚部转换符号，并用q^*表示

对于四元数q = w + xi + yj + zk，它的共轭四元数为

$$q^{\ast }=w-xi-bj-zk$$

同样的按照共轭复数模长的定义，有

$$q^{\ast }q=\Vert \begin{array}{c}q\end{array}\Vert$$

四元数的逆用q^-1表示，将共轭除以模得到

$$q^{-1}=\frac{q^{\ast }}{\Vert \begin{array}{c}q\end{array}\Vert }$$

四元数的逆和实数的倒数存在有趣的对应关系，对于实数a，有

$$a{a}^{-1}=1$$

对于四元数而言，也存在

$$q{q}^{-1}=1$$

四元数与四元数的逆相乘得到单位四元数[1,0]

INFO

虽然四元数不满足交换律，而共轭四元数与四元数的乘积是满足交换律的

$$q^{\ast }q=q{q}^{\ast }=\Vert \begin{array}{c}q\end{array}\Vert$$

对于单位四元数而言，由于它的模长为1，则有

$$q^{-1}=q^{\ast }$$

模

仿照复数的定义，我们可以将四元数q = w + xi + yj + zk的模长定义为

$$\Vert \begin{array}{c}q\end{array}\Vert =\sqrt{w^2+x^2+y^2+z^2}=\sqrt{w^2+{\Vert \begin{array}{c}v\end{array}\Vert }^2}$$

很难在几何上描述四元数的模长，因为它是在四维空间描述三维空间，只需要理解定义即可

纯四元数

如果一个四元数只有虚部，实部为0，那么称这种形式的四元数为纯四元数

$$q=[0,v]$$

因此任意形式的3D向量都可以转换为纯四元数，对于任意3D向量v，都有纯四元数

$$v=[0,\mathrm{v}]$$

对于两个纯四元数q₁、q₂，它们的乘积为

$$q_1{q}_2=[-v_1·v_2,v_1\times v_2]$$

乘法

与标量相乘

与复数相同，四元数与标量的乘积等于标量与四元数每部分都相乘和

$$a(w+xi+yj+zk)=aw+axi+ayj+azk$$

也可以简化为

$$aq=a[w,v]=[aw,av]$$

四元数乘法（叉乘）

分为两种，分别是点乘、叉乘

计算规则与复数乘法相同，但是复数乘法遵循交换律。不用为四元数乘法使用乘号

• 四元数相乘不遵循交换律

$$q_1{q}_2\ne q_2{q}_1$$

• 四元数相乘遵循结合律

$$(q_1{q}_2)q_3=q_1(q_2{q}_3)$$

例如：q₁左乘q₂结果为

$$\begin{array}{r}\\ & q_1{q}_2& \\ & =(w_1+x_{1}i+y_{1}j+z_{1}k)·(w_2+x_{2}i+y_{2}j+z_{2}k)\\ & =w_1{w}_2+w_1{x}_{2}i+w_1{y}_{2}j+w_1{z}_{2}k+\\ & x_{1}i{w}_2+x_{1}i{x}_{2}i+x_{1}i{y}_{2}j+x_{1}i{z}_{2}k+\\ & y_{1}j{w}_2+y_{1}j{x}_{2}i+y_{1}j{y}_{2}j+y_{1}j{z}_{2}k+\\ & z_{1}k{w}_2+z_{1}k{x}_{2}i+z_{1}k{y}_{2}j+z_{1}k{z}_{2}k\\ \\ & =w_1{w}_2+w_1{x}_{2}i+w_1{y}_{2}j+w_1{z}_{2}k+\\ & x_1{w}_{2}i-x_1{x}_2+x_1{y}_{2}k-x_1{z}_{2}j+\\ & y_1{w}_{2}j-y_1{x}_{2}k-y_1{y}_2+y_1{z}_{2}i+\\ & z_1{w}_{2}k+z_1{x}_{2}j-z_1{y}_{2}i-z_1{z}_2\\ \\ & =w_1{w}_2-x_1{x}_2-y_1{y}_2-z_1{z}_2+\\ & (x_1{w}_2+w_1{x}_2-z_1{y}_2+y_1{z}_2)i+\\ & (y_1{w}_2+z_1{x}_2+w_1{y}_2-x_1{z}_2)j+\\ & (z_1{w}_2-y_1{x}_2+x_1{y}_2+w_1{z}_2)k\\ \\ & \end{array}$$

我们可以将结果进一步转化为矩阵形式

$$q_1{q}_2=\left[\begin{array}{cccc}{w}_1& -x_1& -y_1& -z_1\\ x_1& w_1& -z_1& y_1\\ y_1& z_1& w_1& -x_1\\ z_1& -y_1& x_1& w_1\end{array}\right]\left[\begin{array}{c}{w}_2\\ x_2\\ y_2\\ z_2\end{array}\right]$$

其实四元数相乘的本质也是一个线性转换

接下来我们考虑虚部向量形式的点乘和叉乘，则有

• 点乘

$$v_1·v_2=\left[\begin{array}{c}{x}_1\\ y_1\\ z_1\end{array}\right]\left[\begin{array}{c}{x}_2\\ y_2\\ z_2\end{array}\right]=x_1{x}_2+y_1{y}_2+z_1{z}_2$$

• 叉乘

$$v_1\times v_2=\left[\begin{array}{c}{x}_1\\ y_1\\ z_1\end{array}\right]\times \left[\begin{array}{c}{x}_2\\ y_2\\ z_2\end{array}\right]=y_1{z}_2-z_1{y}_2+z_1{x}_2-x_1{z}_2+x_1{y}_2-y_1{x}_2$$

我们将q₁左乘q₂结果再变换下

$$\begin{array}{r}\\ & w_1{w}_2-(x_1{x}_2+y_1{y}_2+z_1{z}_2)+\\ & (x_1{w}_2+w_1{x}_2+y_1{z}_2-z_1{y}_2)i+\\ & (y_1{w}_2+w_1{y}_2+z_1{x}_2-x_1{z}_2)j+\\ & (z_1{w}_2+w_1{z}_2+x_1{y}_2-y_1{x}_2)k\\ \\ & \end{array}$$

观察后可知，存在以下等式

$$q_1{q}_2=[w_1{w}_2-v_1·v_2,w_2{v}_1+w_1{v}_2+v_1\times v_2]$$

这个等式又叫Graβmann Product积

点乘

四元数的点乘计算规则与向量相同，得到的结果是一个标量，对应位置乘积之和

$$q_1·q_2=\left[\begin{array}{c}{w}_1\\ x_1\\ y_1\\ z_1\end{array}\right]\left[\begin{array}{c}{w}_2\\ x_2\\ y_2\\ z_2\end{array}\right]=w_1{w}_2+x_1{x}_2+y_1{y}_2+z_1{z}_2$$

四元数点乘的几何意义与向量点乘的几何意义相似，表示四元数与另一个四元数的"相似"程度

对数运算

四元数对数运算的结果也是一个四元数

对于四元数q，有

$$\begin{array}{r}\\ & {\log }_{}q& \\ & ={\log }_{}\Vert \begin{array}{c}q\end{array}\Vert \frac{q}{\Vert \begin{array}{c}q\end{array}\Vert }& \\ & ={\log }_{}\Vert \begin{array}{c}q\end{array}\Vert +{\log }_{}\frac{q}{\Vert \begin{array}{c}q\end{array}\Vert }& \\ & ={\log }_{}\Vert \begin{array}{c}q\end{array}\Vert +{\log }_{}(\cos \theta +n\sin \theta )\\ & ={\log }_{}\Vert \begin{array}{c}q\end{array}\Vert +n\theta \\ & =\left[\begin{array}{c}{\log }_{}\Vert \begin{array}{c}q\end{array}\Vert \\ n\theta \end{array}\right]\end{array}$$

对应的单位四元数有

$$\left[\begin{array}{c}0\\ n\theta \end{array}\right]$$

INFO

证明需要用到欧拉公式

$$e^{i\theta }=\cos \theta +i\sin \theta$$

幂次运算

四元数可以作为底数，记作q^t，类似实数求幂

$$q^t=e^{t\ln q}$$

当t从0到1时，q从1到q；当t从1到0时，q从q到1

类似的，对应四元数，当t从0到1时，q从[1, 0]到[q, 0]；当t从1到0时，q从[q, 0]到[1, 0]

例如，如果一个四元数q表示一个角位移，那么q^1/3表示这个角位移的1/3部分

相应的，如果四元数q代表绕旋转轴顺时针旋转θ角度，则q²表示2θ角度的顺时针旋转，q^-1表示θ角度的逆时针旋转

一般来说，凡事涉及到指数运算的代数公式，如

$$(a^s)t=a^{st}$$

在四元数的幂次运算中都是不适用的

const power = function (w, x, y, z, time) {
  const alpha = Math.acos(w);
  const newAlpha = alpha * time;
  const mult = Math.sin(newAlpha) / Math.sin(alpha);
  return [Math.cos(newAlpha), x * mult, y * mult, z * mult];
};

与3D旋转

3D中的任意角位移都可以通过绕任意轴的单一旋转来完成，轴-角对表示为(n,θ)

实际上，轴-角对是表示旋转的第四种方式，但是在描述轴-角对时一般被欧拉角和四元数替代了

向量形式

任意向量v绕单位向量n旋转θ，用四元数表示为

$$q=\left[\begin{array}{cc}\cos \frac{\theta }{2}& n\sin \frac{\theta }{2}\end{array}\right]=\left[\begin{array}{cccc}\cos \frac{\theta }{2}& n_x\sin \frac{\theta }{2}& n_y\sin \frac{\theta }{2}& n_z\sin \frac{\theta }{2}\end{array}\right]$$

旋转后的向量可以使用四元数乘法来获得，令

$$v=[0,\mathrm{v}]$$

则转换后后的向量v^'（证明参考3.2章节）为

$$v^{{}^{\prime }}=qv{q}^{\ast }=qv{q}^{-1}$$

则有

$$v^{{}^{\prime }}=[0,\cos \theta \mathrm{v}+(1-\cos \theta )(\mathrm{u}·\mathrm{v})\mathrm{u}+\sin \theta (\mathrm{u}\times \mathrm{v})]$$

矩阵形式

指数形式

获取旋转角度θ、旋转轴

如果有一个四元数q = [w, v]表示的旋转，那么它对应的旋转角度为

$$\frac{\theta }{2}=\arccos w$$

对应的旋转轴为

$$n=\frac{v}{sin(\arccos w)}=\frac{v}{sin\frac{\theta }{2}}$$

旋转的复合

如果有两个绕着不同旋转轴，不同旋转角度的四元数q₁、q₂，向量为v，最终旋转向量为v^'，则有

$$v^{{}^{\prime }}=q_2{q}_{1}v{q}_1^{\ast }{q}_2^{\ast }$$

推广到n个旋转，则有

$$v^{{}^{\prime }}=q_n{q}_{n-1}\cdots q_2{q}_{1}v{q}_1^{\ast }{q}_2^{\ast }\cdots q_{n-1}^{\ast }{q}_n^{\ast }$$

插值

在两个变换之间插入变换，可以让变换更加平滑

slerp

可以在两个四元数之间平滑插值，而且它避免了欧拉角插值的所有问题

开始和结束的四元数分别是q⁰、q¹，插值参数设为变量t，t在0和1之间变化，表示为slerp(q⁰,q⁰,t)

$$slerp(q_0,q_0,t)=q_0(q_0^{-1}{q}_1{)}^t$$

这是理论上的表达式，但是实践中有更有效的计算方式

w为q⁰、q¹的夹角，有

$$slerp(q_0,q_0,t)=\frac{\sin ((1-t)w)}{\sin w}{q}_0+\frac{\sin (tw)}{\sin w}{q}_1$$

let w0, x0, y0, z0; // 四元数1
let w1, x1, y1, z1; // 四元数2
let t; // 插值变量

// 首先用点乘判断这两个四元数之间的夹角是否为钝角
let cosOmega = w0 * w1 + x0 * x1 + y0 * y1 + z0 * z1;
if (cosOmega < 0) {
  //  为钝角时则将其中一个转换为负值
  w0 = -w0;
  x0 = -x0;
  y0 = -y0;
  z0 = -z0;
  cosOmega = -cosOmega;
}

let k0, k1;
// 如果两个四元数过于接近，则判定为为线性插值
if (cosOmega > 0.9999) {
  k0 = 1 - t;
  k1 = t;
} else {
  const sinOmega = Math.sqrt(1 - cosOmega ** 2);
  const omega = Math.atan2(sinOmega, cosOmega);
  const oneOverSinOmega = 1 / sinOmega;
  k0 = Math.sin((1 - t) * omega) * oneOverSinOmega;
  k1 = sin(t * omega) * oneOverSinOmega;
}
// 插值
w = w0 * k0 + w1 * k1;
x = x0 * k0 + x1 * k1;
t = y0 * k0 + y1 * k1;
z = z0 * k0 + z1 * k1;

squad

slerp提供了两个方位之间的插值，当多于两个方位的插值时需要使用squad

$$s_i=e^{-\frac{{\log }_{}{q}_{i+1}{q}_i^{-1}+{\log }_{}{q}_{i-1}{q}_i^{-1}}{4}}{q}_i$$$$squad(q_i,q_{i+1},s_i,s_{i+1},h)=slerp(slerp(q_i,q_{i+1},h),slerp(s_i,s_{i+1},h),2h(1-h))$$

优缺点

优点

• 可以平滑插值，另外两种方式都无法插值
• 快速连接和角位移求逆
  • 四元数叉乘可以快速的将转换序列组合称一个转换，而矩阵效率低一些
  • 共轭四元数提供了反角位移更加简便的方式，矩阵的转置矩阵也可以快速计算反角位移下的旋转，但是没有四元数快
• 可以和矩阵形式快速转换，四元数与矩阵形式的相互转换高于欧拉角与矩阵的相互转换效率
• 占用空间低，仅用四个数
  • 欧拉角需要3个数(θ,γ,β)，四元数需要4个数（w,x,y,z），矩阵需要9个数

缺点

• 四元数可能不合法，由于精度丢失、坏数据点等问题导致四元数不可用，但是可以通过四元数标准化解决
• 难于使用，相对于矩阵、欧拉角，四元数相对编码要求高

参考：

【1】Understanding Quaternions

【2】四元数与空间旋转

【3】四元数与三维旋转

【4】四元数的可视化

【5】如何形象地理解四元数？

【6】四元数速查手册

【7】欧拉公式