射线与其他图元

本文探讨射线与其他图元的相交性检测，包括平面、圆/球、三角形、AABB边界框等几何图元

与平面

射线的参数定义：

$$\mathrm{p}(t)={\mathrm{p}}_0+t\mathrm{d}$$

平面的定义为：

$$\mathrm{p}·\mathrm{n}=d$$

这里不限制射线定义中的方向向量d和平面定义中的向量n是单位向量，而且不限制射线的长度，假设它为无限延伸的，则两者交点处

$$({\mathrm{p}}_0+t\mathrm{d})·\mathrm{n}=d\Rightarrow t=\frac{d-{\mathrm{p}}_0·\mathrm{n}}{\mathrm{d}·\mathrm{n}}$$

• 这里我们仅讨论了射线方向与平面法向量方向相反的情况，即d·n < 0
• 如果t有范围限制，计算出的t值不再范围内，那么意味着射线和平面是不相交的。
• 射线与平面平行，则向量d和向量n平行，即点乘为0，那么它们之间没有交点

与圆/球

这里我们假设向量d为单位向量，t从0到l变换，l为射线长度

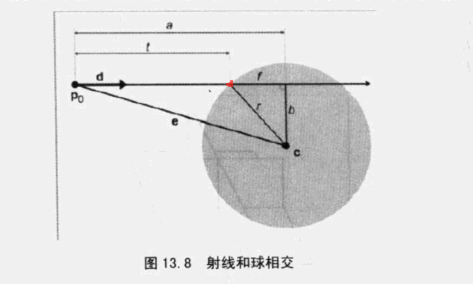
根据图形可知存在以下等式

$$a=t+f$$$$a^2=e^2+b^2$$

向量e在向量d上的投影长度为标量a，而且由于向量d为单位向量，那么有

$$a=\mathrm{e}·\mathrm{d}$$

根据以上等式，得出标量t的表达式为

$$t=a-f=\mathrm{e}·\mathrm{d}-\sqrt{r^2-b^2}=\mathrm{e}·\mathrm{d}-\sqrt{r^2-(e^2-a^2)}=\mathrm{e}·\mathrm{d}-\sqrt{r^2-e^2+a^2}$$

• r²-e²+a²的值为负数时，表示无交点
• 射线的起点也可能在圆内，此时e²<r²

三角形

判断射线与三角形的是否相交分为两步：

1. 计算射线与三角形所在平面的交点
2. 计算交点的重力坐标，判断交点是否在三角形内部

一些编码技巧

1. 尽可能早的返回值
2. 尽可能延迟“昂贵”的运算，如除法
3. 只检测与三角形正面相交

AABB边界框

射线与AABB边界框是否相交，可以有效简化射线与物体的相交性判断，在实践中具有重要意义。

例如：射线与一组三角形网格构成的物体的相交性，可以优先判断与物体的边界框是否相交，进而无需挨个判断射线与这个物体所有三角形的相交性

Woo提出了一种判断相交性的方法：

1. 判断射线会与边界框的哪个平面相交
2. 计算出交点
3. 如果交点在边界框中，那么相交，反之则不相交