三角形

三角形在计算机图形学中应用广泛，复杂的3D表面都是用一个个三角形组成的网格模拟的。

基本性质

对于任意三角形

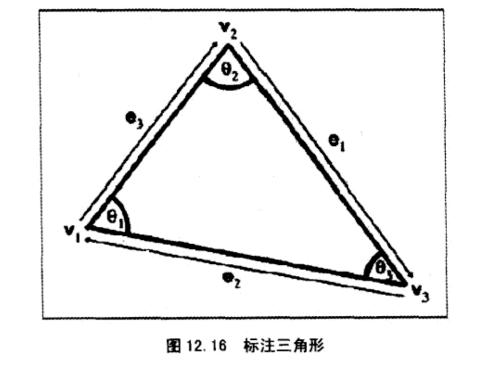
$img.png$

\begin{aligned} l_{1} = v_{3} - v_{2} & l_{1} = ‖ \begin{array}{c} e 1 \end{array} ‖ \end{aligned}

\begin{aligned} l_{2} = v_{1} - v_{3} & l_{2} = ‖ \begin{array}{c} e 2 \end{array} ‖ \end{aligned}

\begin{aligned} l_{3} = v_{2} - v_{1} & l_{3} = ‖ \begin{array}{c} e 3 \end{array} ‖ \end{aligned}

正弦公式

\frac{l_{1}}{\sin θ_{1}} = \frac{l_{2}}{\sin θ_{2}} = \frac{l_{3}}{\sin θ_{3}} = 2 R

R为三角形外接圆的半径

余弦公式

l_{1}^{2} = l_{2}^{2} + l_{3}^{2} - 2 l_{2} l_{3} \cos θ_{1}

l_{2}^{2} = l_{3}^{2} + l_{1}^{2} - 2 l_{3} l_{1} \cos θ_{2}

l_{3}^{2} = l_{2}^{2} + l_{1}^{2} - 2 l_{2} l_{1} \cos θ_{3}

周长

三个边相加即三角形的周长

C = l_{1} + l_{2} + l_{3}

面积

如果知道三角形的高为h，底边长度为b，那么有

A r e a = \frac{1}{2} b h

如果只知道三角形的三个边长，而不知道高度，那么可知

假设s为周长的一半

s = \frac{l_{1} + l_{2} + l_{3}}{2}

A r e a = \sqrt{s (s - l_{1}) (s - l_{2}) (s - l_{3})}

INFO

这称为海伦公式，在3D中使用非常方便

但是在3D中经常只知道点对应的笛卡尔坐标，当然也可以通过计算出边长再带入海伦公式计算面积，但是为了避免复杂计算，我们可以通过以下方式计算

基本思想是：每个向量与x轴围成直角梯形的“有符号”面积之和，如果边的端点是从左到右则面积为正，反之则面积为负

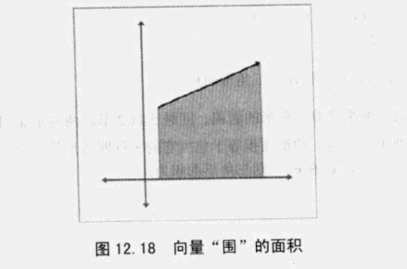
$img.png$

A (e_{1}) = \frac{(y_{2} + y_{3}) (x_{3} - x 2)}{2}

A (e_{2}) = \frac{(y_{3} + y_{1}) (x 1 - x_{3})}{2}

A (e_{3}) = \frac{(y_{2} + y_{1}) (x_{2} - x 1)}{2}

\begin{aligned} A r e a \\ = A (e_{1}) + A (e_{2}) + A (e_{3}) \\ = \frac{(y_{1} - y_{3}) (x_{2} - x_{3}) + (y_{2} - y_{3}) (x_{3} - x_{1})}{2} \end{aligned}

INFO

上述是y坐标平移y₃后简化过的公式，因为平移并不会改变三角形的面积

这个思想同样适用于多边形

叉乘计算，我们已经知道叉乘的几何意义是向量围成的平行四边形的面积，那么它的一半也即是三角形的面积

A r e a = \frac{‖ \begin{matrix} e_{1} \times e_{2} \end{matrix} ‖}{2}

其中e₁、e₂是三角形的任意两个边向量

重心坐标空间

在标准3D空间中平移和转换任意方向的三角形是很复杂的，为了降低计算的复杂度，我们引入一个坐标空间，这个坐标空间与三角形的点有关，称这个空间为重心坐标空间，又称为面积坐标。重心坐标是齐次坐标（投影坐标）的一种。

重心坐标空间与标准3D坐标之间的转换规则：

(b_{1}, b_{2}, b_{3}) \Leftrightarrow b_{1} v_{1} + b_{2} v_{2} + b_{3} v_{3}

而且满足

b_{1} + b_{2} + b_{3} = 1

其中b₁、b₂、b₃分别表示v₁、v₂、v₃对该点的权重

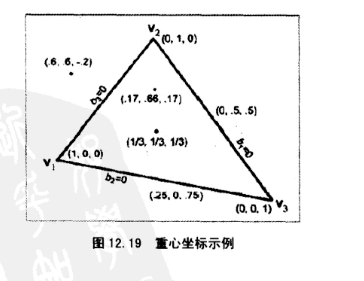
$img.png$

在重心坐标空间中我们用3个变量表示一个2D坐标，但是我们已知b₁+b₂+b₃=1，其实只需要知道两个值便可以计算出另外一个坐标，因此它有2个自由度

2D

已知重心坐标空间下的坐标，计算标准3D坐标的坐标

只需要三角形的三个点带入即可转换为标准3D坐标

b_{1} v_{1} + b_{2} v_{2} + b_{3} v_{3}

已知标准3D坐标的坐标，计算重心坐标空间下的坐标

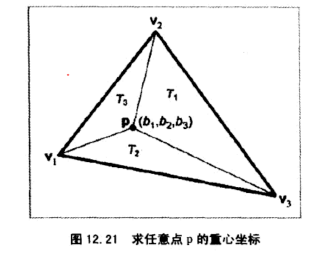
$img.png$

我们的目标是计算出b₁、b₂、b₃，根据转化公式有

p_{x} = b_{1} x_{1} + b_{2} x_{2} + b_{3} x_{3}

p_{y} = b_{1} y_{1} + b_{2} y_{2} + b_{3} y_{3}

b_{1} v_{1} + b_{2} v_{2} + b_{3} v_{3} = 1

计算出

b_{1} = \frac{(p_{y} - y_{3}) (x_{2} - x_{3}) + (y_{2} - y_{3}) (x_{3} - p_{x})}{(y_{1} - y_{3}) (x_{2} - x_{3}) + (y_{2} - y_{3}) (x_{3} - x_{1})}

b_{2} = \frac{(p_{y} - y_{1}) (x_{3} - x_{1}) + (y_{3} - y_{1}) (x_{1} - p_{x})}{(y_{1} - y_{3}) (x_{2} - x_{3}) + (y_{2} - y_{3}) (x_{3} - x_{1})}

b_{3} = \frac{(p_{y} - y_{2}) (x_{1} - x_{2}) + (y_{1} - y_{2}) (x_{2} - p_{x})}{(y_{1} - y_{3}) (x_{2} - x_{3}) + (y_{2} - y_{3}) (x_{3} - x_{1})}

根据面积公式，最终简化为

b_{1} = \frac{A_{1}}{A}

b_{2} = \frac{A_{2}}{A}

b_{3} = \frac{A_{3}}{A}

点p在三角形外部也适用，子三角形的点是顺时针时，面积为正，反之则为负

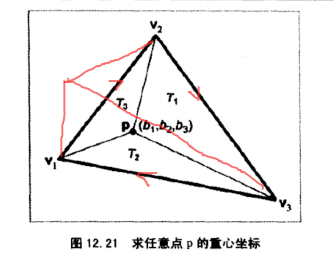
$img.png$

子三角形的三个点共线（即在三角形边上），则对应的重力空间坐标为0

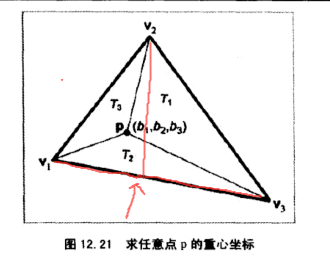
$img.png$

3D

3D中任意点的坐标转化为重力空间下的坐标是复杂的，原因有

在3D中根据点坐标可以列出4个方程，但是要计算出3个值
任意点的坐标并不一定在三角形平面上，这是重力坐标没有意义

我们可以通过投影将3D问题转化为2D问题，抛弃3D坐标中的一个自由度，那么如何选择需要抛弃的自由度呢？

首先计算出三角形平面的法向量，并确定法向量坐标中绝对值最大的坐标，例如：三角形所在平面的法向量为[0, 0, 1]，那么则抛弃z轴上的自由度，并将三角形投影到xy平面上

代码示例：

import { Vector3, Vector3Helper } from './Vector3';

/**
 * 通过投影减少自由度到2D的方式将3D坐标转化为重力空间坐标
 *
 * @param v 按照顺时针顺序排列好的三角形向量
 * @param p 3D空间中任意一点
 * @return b 转换后的重力空间下的坐标
 */
export function computeBarycentricCoords3d(
  v: [Vector3, Vector3, Vector3],
  p: Vector3,
): [number, number, number] | undefined {
  //   计算两个边向量，按顺时针方向
  const d1 = v[1].subtract(v[0]);
  const d2 = v[2].subtract(v[1]);

  // 计算出三角形平面的法向量
  // 不需要标准化
  const n = Vector3Helper.crossProduct(d1, d2);

  // 选择投影平面
  const max = Math.max(Math.abs(n.x), Math.abs(n.y), Math.abs(n.z));

  // 计算出子式
  let u1, u2, u3, u4;
  let v1, v2, v3, v4;

  switch (max) {
    case Math.abs(n.x):
      // 抛弃x，投影到yz平面
      u1 = v[0].y - v[2].y;
      u2 = v[1].y - v[2].y;
      u3 = p.y - v[0].y;
      u4 = p.y - v[2].y;

      v1 = v[0].z - v[2].z;
      v2 = v[1].z - v[2].z;
      v3 = p.z - v[0].z;
      v4 = p.z - v[2].z;
      break;
    case Math.abs(n.y):
      // 抛弃y，投影到xz平面
      u1 = v[0].z - v[2].z;
      u2 = v[1].z - v[2].z;
      u3 = p.z - v[0].z;
      u4 = p.z - v[2].z;

      v1 = v[0].x - v[2].x;
      v2 = v[1].x - v[2].x;
      v3 = p.x - v[0].x;
      v4 = p.x - v[2].x;
      break;
    case Math.abs(n.z):
      // 抛弃z，投影到xy平面
      u1 = v[0].x - v[2].x;
      u2 = v[1].x - v[2].x;
      u3 = p.x - v[0].x;
      u4 = p.x - v[2].x;

      v1 = v[0].y - v[2].y;
      v2 = v[1].y - v[2].y;
      v3 = p.y - v[0].y;
      v4 = p.y - v[2].y;
      break;
  }

  const denom = v1 * u2 - v2 * u1;
  if (denom !== 0) {
    const oneOverDenom = 1 / denom;
    const b1 = (v4 * u2 - v2 * u4) * oneOverDenom;
    const b2 = (v1 * u3 - v3 * u1) * oneOverDenom;
    const b3 = 1 - b1 - b2;
    return [b1, b2, b3];
  }
}

另一种方式是根据叉乘的几何意义计算各个子三角形的面积值，再进行计算。但是这样存在一个缺点：叉乘的大小永远是正的，我们可以通过点乘来解决这个问题

首先我们假设向量c为三角形任意两条边的叉乘，它的长度是三角形面积的2倍，引入一个单位向量n，与向量c保持平行，那么

c \cdot n = ‖ \begin{matrix} c \end{matrix} ‖ ‖ \begin{matrix} n \end{matrix} ‖ \cos θ = \pm ‖ \begin{matrix} c \end{matrix} ‖

将上述面积再除以2，就得到的三角形面积的“有符号”值，利用这个思想，我们依次计算出各个子三角形的面积值

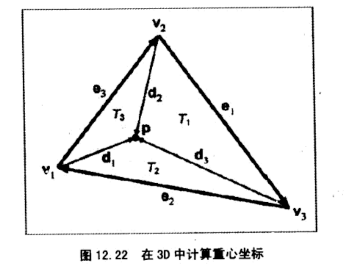
$img.png$

取e₁、e₂计算出单位向量n

n = \frac{e_{1} \times e_{2}}{‖ \begin{matrix} e_{1} \times e_{2} \end{matrix} ‖}

A = \frac{(e_{1} \times e_{2}) \cdot n}{2}

A (T_{1}) = \frac{(e_{1} \times (p - v_{3})) \cdot n}{2}

A (T_{2}) = \frac{(e_{2} \times (p - v_{1})) \cdot n}{2}

A (T_{1}) = \frac{(e_{3} \times (p - v_{2})) \cdot n}{2}

则计算出对应的权重为

b_{1} = \frac{A (T_{1})}{A} = \frac{(e_{1} \times (p - v_{3})) \cdot n}{(e_{1} \times e_{2}) \cdot n}

b_{2} = \frac{A (T_{2})}{A} = \frac{(e_{2} \times (p - v_{1})) \cdot n}{(e_{1} \times e_{2}) \cdot n}

b_{3} = \frac{A (T_{3})}{A} = \frac{(e_{3} \times (p - v_{2})) \cdot n}{(e_{1} \times e_{2}) \cdot n}

不必标准化n，分母为n·n

特殊点

重心

三角形的最佳平衡点，每条边中线的交叉点为重心，又称为质心

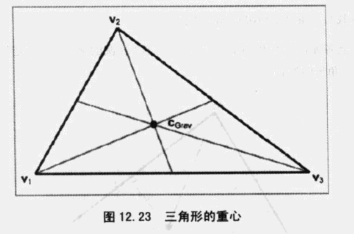
$img.png$

标准3D坐标系下的计算公式

c_{g r a v} = \frac{v_{1} + v_{1} + v_{1}}{3}

对应的重心坐标系下

c_{g r a v} = (\frac{1}{3}, \frac{1}{3}, \frac{1}{3})

内心

到三条边距离都相等的点，也是三角形内切圆的圆心，也是3个角平分线的交点

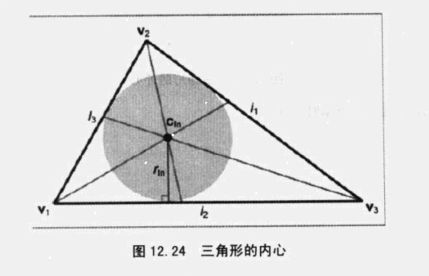
$img.png$

标准3D坐标系下的计算公式

c_{i n} = \frac{l_{1} v_{1} + l_{2} v_{2} + l_{3} v_{3}}{l_{1} + l_{2} + l_{3}}

对应的重心坐标系下

c_{i n} = (\frac{l_{1}}{l_{1} + l_{2} + l_{3}}, \frac{l_{2}}{l_{1} + l_{2} + l_{3}}, \frac{l_{3}}{l_{1} + l_{2} + l_{3}})

内切圆的半径可以通过面积除以周长取得

r_{i n} = \frac{S}{l_{1} + l_{2} + l_{3}}

外心

外心是到各顶点距离相等的点

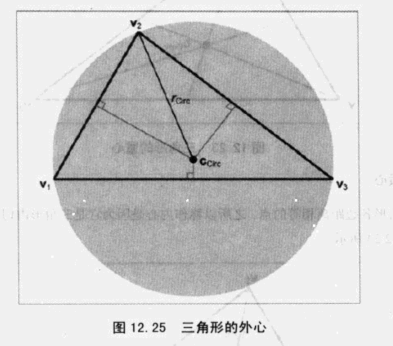
$img.png$

首先给出以下子式

\begin{aligned} d_{1} = - e_{2} e_{3} \\ d_{2} = - e_{3} e_{1} \\ d_{3} = - e_{1} e_{2} \\ c_{1} = d_{2} d_{3} \\ c_{2} = d_{3} d_{1} \\ c_{3} = d_{1} d_{2} \\ c = c_{1} + c_{2} + c_{3} \end{aligned}

标准3D坐标系下的计算公式

c_{C i r c} = \frac{(c_{2} + c_{3}) v_{1} + (c_{3} + c_{1}) v_{2} + (c_{1} + c_{2}) v_{3}}{2 c}

对应的重心坐标系下

c_{C i r c} = (\frac{c_{2} + c_{3}}{2 c}, \frac{c_{3} + c_{1}}{2 c}, \frac{c_{1} + c_{2}}{2 c})

外接圆的半径为

r_{C i r c} = \frac{\sqrt{\frac{(d_{1} + d_{2}) (d_{2} + d_{3}) (d_{3} + d_{1})}{c}}}{2}

参考：

【1】三角学#标准恒等式

【2】海伦公式

【3】重心坐标

矩阵与线性变换

3D中的方位与角位移

四元数

代码实现

几何图元

几何检测

最近点

相交性检测

图形数学

可见行检测

三角形

基本性质

正弦公式

余弦公式

周长

面积

重心坐标空间

2D

3D

特殊点

重心

内心

外心

四元数

最近点

相交性检测

三角形 ​

基本性质 ​

正弦公式 ​

余弦公式 ​

周长 ​

面积 ​

重心坐标空间 ​

2D ​

3D ​

特殊点 ​

重心 ​

内心 ​

外心 ​

三角形

基本性质

正弦公式

余弦公式

周长

面积

重心坐标空间

2D

3D

特殊点

重心

内心

外心