坐标空间

从物体的角度，按照坐标空间在渲染管道中出现的顺序介绍

模型与世界空间

物体首先在物体空间（又称为模型空间、局部空间）中，常见的信息有顶点位置和表面法向量

将坐标从物体空间中转换到世界空间中，这个过程被称为模型变换。通常，光照计算使用的是世界空间，但其实使用什么坐标空间都无所谓，只需要保证光照和物体处于一个空间中即可。

摄像机空间

通过视变换，顶点从世界空间变换到摄像机空间（又称为眼睛空间）

摄像机空间的原点是投影中心，一个轴是平行于投影方向、垂直于投影面，另一个轴是由上、下面相交得到，最后一个轴则是左右面相交得到。

如果我们考虑的是透视空间，那么一个轴可以认为是水平的，另一个轴可以认为是垂直的

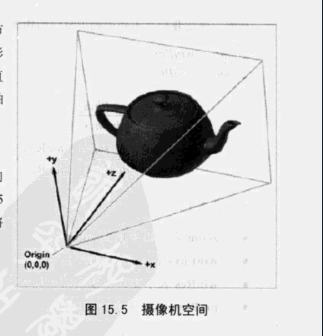
对于左手坐标系，常约定摄像机指向的方向为+z，+x指向右方向，+y指向上方向

裁剪空间

接着由变换到裁剪空间（又称为标准视体空间），变换的矩阵被称为裁剪矩阵

根据使用4x4矩阵进行透视投影章节中的描述，将3D空间中的点投影到z=d投影平面上，对应的投影矩阵为

$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& \frac{1}{d}\\ 0& 0& 0& 0\end{array}\right]$$

我们知道相机中焦距发生改变时会对成像大小造成影响，具体的影响是

• 焦距变大，图像更大
• 焦距变小，图像更小

但是对于计算机而言，却不是如此的。当d发生改变时，视锥体的形状、投影平面的大小会发生改变。

那么就会导致在输出屏幕给定的前提下，成像的大小是不变的，那么就意味着d值的大小并不会对成像造成影响，为了方便起见，我们令d=1

那么投影矩阵可以简化为

$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 1\\ 0& 0& 0& 0\end{array}\right]$$

那么对齐次空间中的向量[x y z 1]进行透视投影，则有

$$\left[\begin{array}{cccc}x& y& z& 1\end{array}\right]·\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 1\\ 0& 0& 0& 0\end{array}\right]=\left[\begin{array}{cccc}x& y& z& z\end{array}\right]\Rightarrow \left[\begin{array}{ccc}\frac{x}{z}& \frac{y}{z}& 1\end{array}\right]$$

假设zoom_x、zoom_y分别为水平、垂直方向上的缩放值，设n、f分别是近、远剪切面的距离

OpenGL风格的DIP矩阵如下，这里近裁剪面到远裁剪面的z值在[-w,w]之间

$$\left[\begin{array}{cccc}zoo{m}_x& 0& 0& 0\\ 0& zoo{m}_y& 0& 0\\ 0& 0& \frac{f+n}{f-n}& 1\\ 0& 0& \frac{2nf}{n-f}& 0\end{array}\right]$$

DirectX风格的DIP矩阵如下，这里近裁剪面到远裁剪面的z值在[0,w]之间

$$\left[\begin{array}{cccc}zoo{m}_x& 0& 0& 0\\ 0& zoo{m}_y& 0& 0\\ 0& 0& \frac{f}{f-n}& 1\\ 0& 0& \frac{nf}{n-f}& 0\end{array}\right]$$

屏幕空间

视锥体完成了几何体的裁剪之后，需要将几何体投影到屏幕空间，输出窗口的大小并不一定要等于屏幕大小，只需要保证比例相等即可

参考

【1】裁剪矩阵推导