向量

数学定义

在数学中区分为向量和标量，其中标量有大小，向量既有大小又有方向，例如：速度、位移等都是向量，速率、长度等是标量。

几何定义

向量可以表示为位移序列，例如[1,2,3]表示为在三维坐标系中向x轴右移1个位置，y轴上移2个位置，z轴前移3个位置。位移顺序无关，最终得到点的位置是相同的

向量与点

向量与点的区别：向量记录点的位移量，而点记录的是位置信息

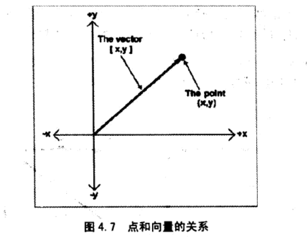
$img.png$

大多数情况下，位移都是从原点开始的，但是也存在位移并不是从原点开始的情况。

向量运算

零向量

零向量是唯一一个没有方向的向量，但是不能将它理解为一个点，而是应该理解为一个没有位移的向量

负向量

- [\begin{matrix} a_{1} \\ a_{2} \\ ⋮ \\ a_{n - 1} \\ a_{n} \end{matrix}] = [\begin{matrix} - a_{1} \\ - a_{2} \\ ⋮ \\ - a_{n - 1} \\ - a_{n} \end{matrix}]

几何解释

负向量是原向量对应的一条反方向的、大小相同的向量

长度

代数公式：

‖ \begin{matrix} v \end{matrix} ‖ = \sqrt{v_{1}^{2} + v_{2}^{2} + \dots + + v_{n - 1}^{2} + v_{n}^{2}}

‖ \begin{matrix} v \end{matrix} ‖ = \sqrt{\sum_{i = 1}^{n} v_{i}^{2}}

几何解释

对于任意向量v，都可以构造出以v为斜边的直角三角形，并通过勾股定理计算三角形斜边的长度

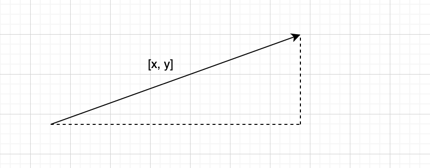
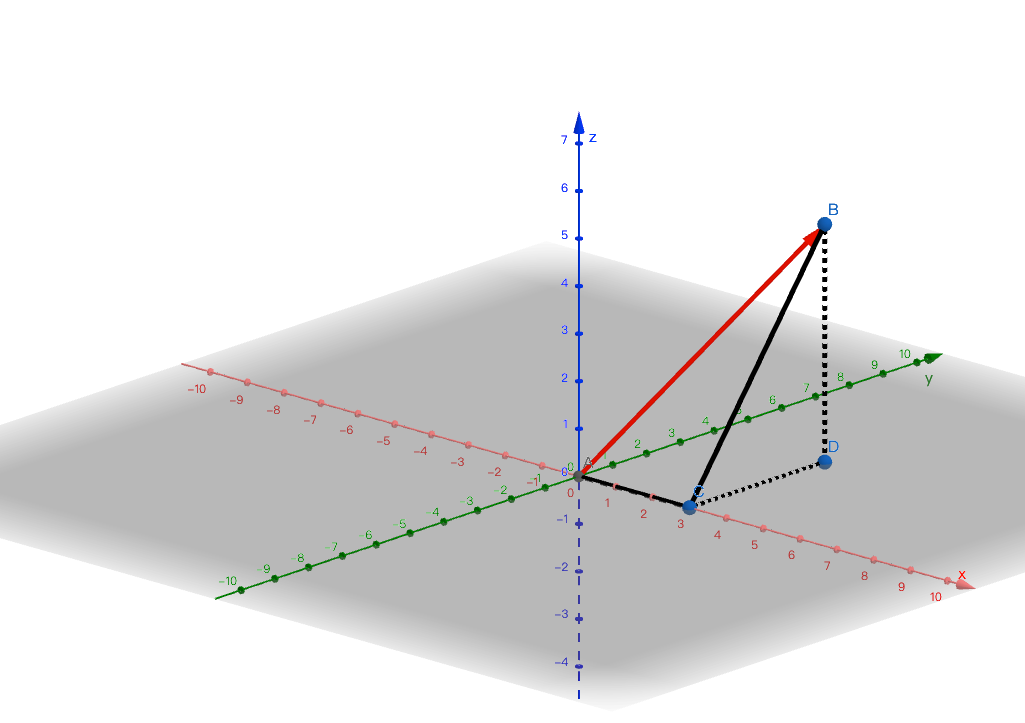
$img.png$

推广到三维坐标系下

$img.png$

标量与向量的乘积

将标量挨个与向量中的值相乘。

k [\begin{matrix} a_{1} \\ a_{2} \\ ⋮ \\ a_{n - 1} \\ a_{n} \end{matrix}] = [\begin{matrix} a_{1} \\ a_{2} \\ ⋮ \\ a_{n - 1} \\ a_{n} \end{matrix}] k = [\begin{matrix} k a_{1} \\ k a_{2} \\ ⋮ \\ k a_{n - 1} \\ k a_{n} \end{matrix}]

负向量本质上是值为-1的标量与原向量相乘得到

几何解释

向量的放缩

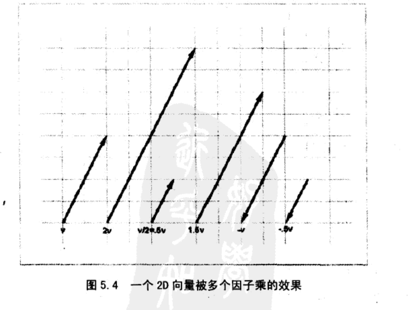
$img.png$

WARNING

向量不能除以向量，标量不能除以向量

标准化

向量中的值除以向量的长度，最终得到标准化后的向量，任何向量标准化后的取值范围在0～1之间

v_{n o r m} = \frac{v}{‖ \begin{matrix} v \end{matrix} ‖}, v \neq 0

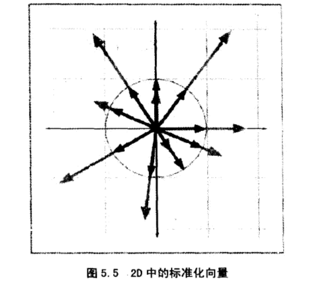
几何解释

标准化后的向量一定在长度为1的单位圆内（在三维坐标中是单位球）

$img.png$

加减规则

相同维度的向量支持相互加减，结果的维度与原向量维度相同。两个向量相加减，将向量中对应维度的值相加减即可。其中减法可以理解为加一个负向量

[\begin{matrix} a_{1} \\ a_{2} \\ ⋮ \\ a_{n - 1} \\ a_{n} \end{matrix}] + [\begin{matrix} b_{1} \\ b_{2} \\ ⋮ \\ b_{n - 1} \\ b_{n} \end{matrix}] = [\begin{matrix} a_{1} + b_{1} \\ a_{2} + b_{2} \\ ⋮ \\ a_{n - 1} + b_{n - 1} \\ a_{n} + b_{n} \end{matrix}]

几何解释

加法满足交换律：向量AB+向量AC=向量AC+向量AB。将向量AC平移到与AB尾部相连，相加的到的向量则是AD

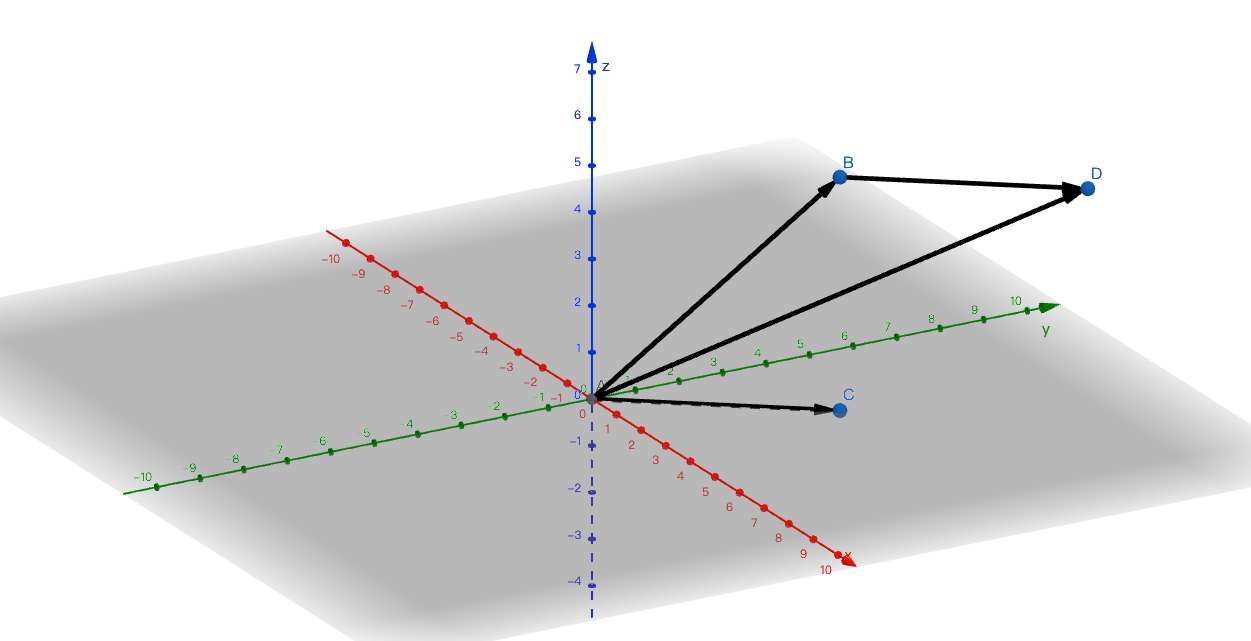
$img.png$

但是减法不满足交换律：向量AB-向量AC 与向量AC-向量AB计算结果不同

向量AB-向量AC=向量CB 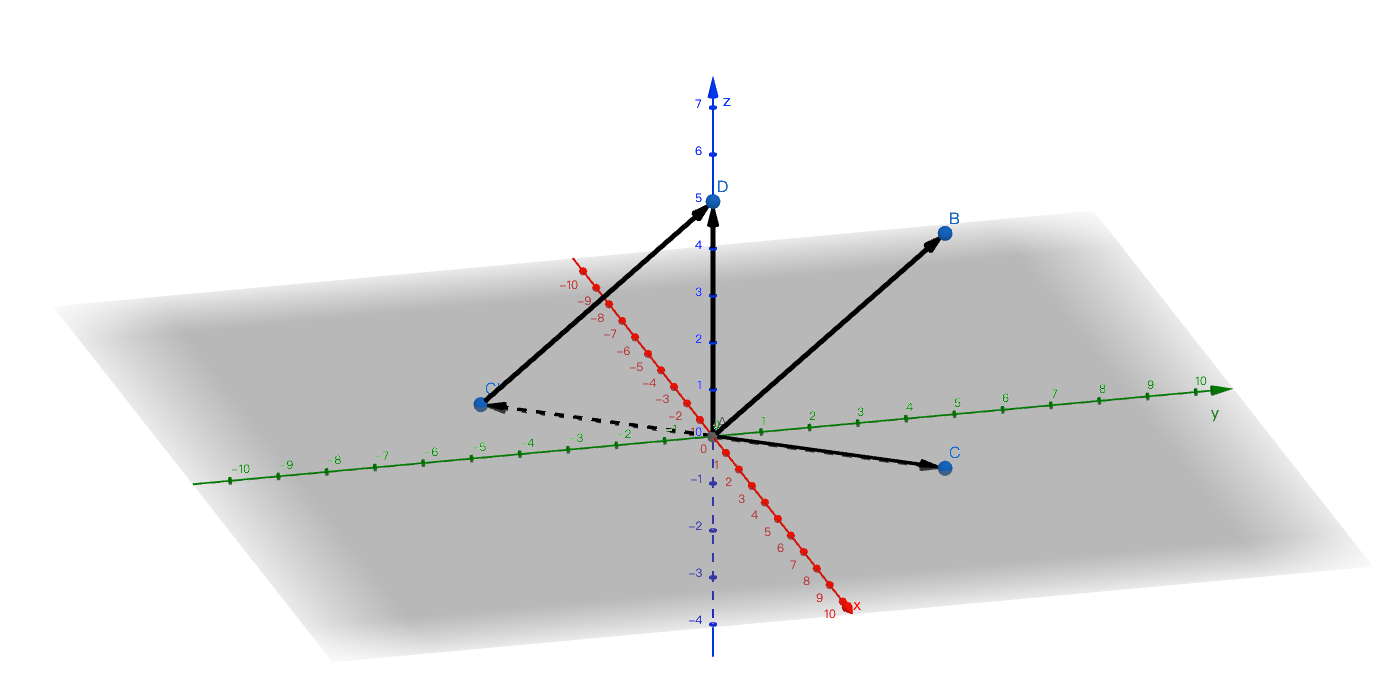$img.png$

向量AC-向量AB=向量BC 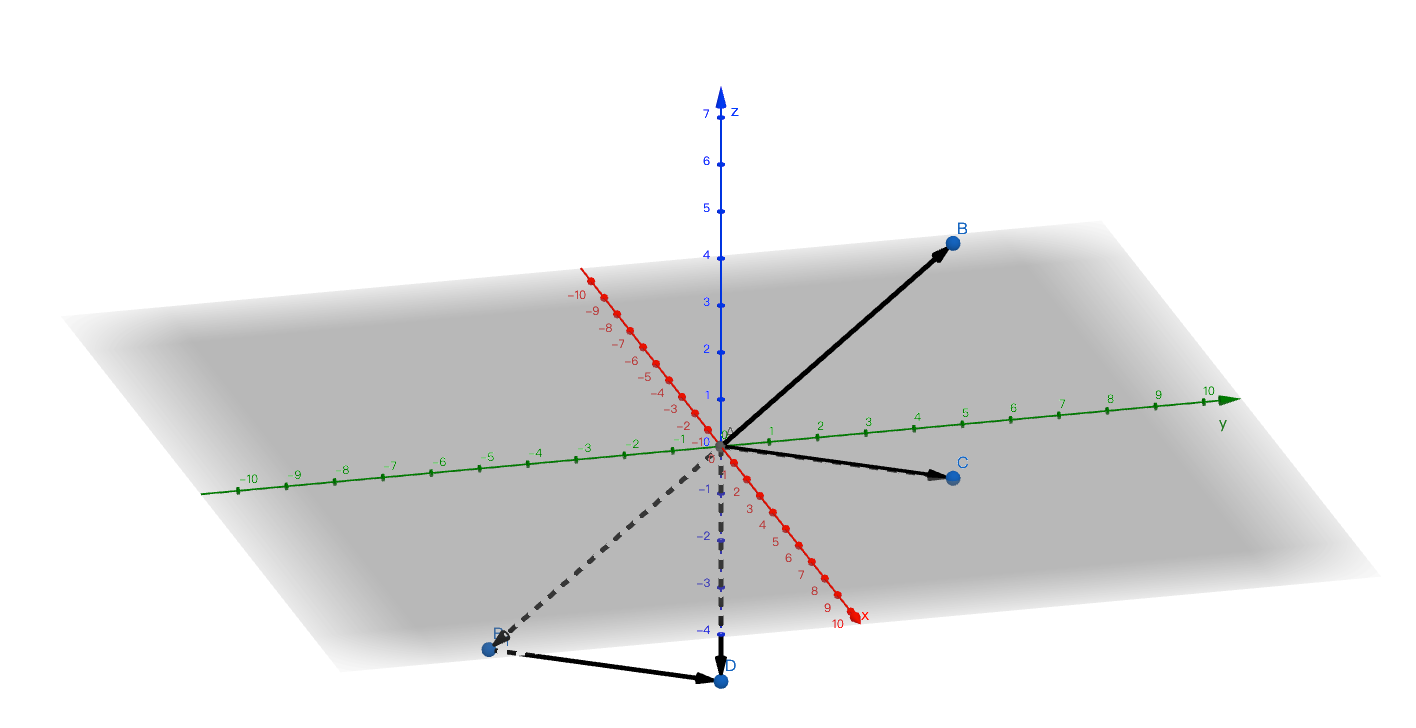$img.png$

这也可以解释向量的位移序列 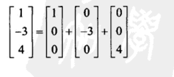$img.png$

INFO

两向量相减，计算出长度即是两向量之间距离

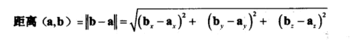
$img.png$

点乘

又称为内积，两个相同维度的向量依据位置挨个相乘，将每个值相加的结果为点乘

[\begin{matrix} a_{1} \\ a_{2} \\ ⋮ \\ a_{n - 1} \\ a_{n} \end{matrix}] \cdot [\begin{matrix} b_{1} \\ b_{2} \\ ⋮ \\ b_{n - 1} \\ b_{n} \end{matrix}] = a_{1} \cdot b_{1} + a_{2} \cdot b_{2} + \dots + a_{n - 1} \cdot b_{n - 1} + a_{n} \cdot b_{n}

几何解释

点乘结果描述的是两个向量的“相似”程度，值越大越相似，返回的是一个标量

v \cdot n = ‖ \begin{matrix} v \end{matrix} ‖ \cdot ‖ \begin{matrix} n \end{matrix} ‖ \cdot \cos θ

等价于

v \cdot n = ‖ \begin{matrix} v \end{matrix} ‖ \cdot \cos θ \cdot ‖ \begin{matrix} n \end{matrix} ‖

其中向量v的长度 * cosθ为向量v在向量n方向上的投影

水平投影和垂直投影

给定向量v，向量n。可以将向量v分解成两个向量，这两个向量分别垂直、平行于向量v

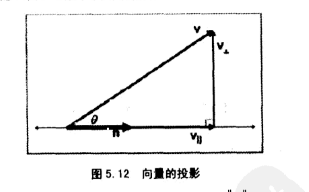
$img.png$

平行方向的向量： $img.png$

垂直方向的向量：

如果将向量n标准化之后，则向量n变为单位向量，长度为1，简化后的n向量垂直方向的向量计算公式为

text

水平分量 + 垂直分量 = 向量v

====>
垂直分量 = 向量v - 水平分量

叉乘

仅可用于三维向量，不满足交换律、结合律，但是满足反交换律

text

向量v x 向量n = -(向量n x 向量v)

代数计算公式：

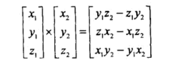
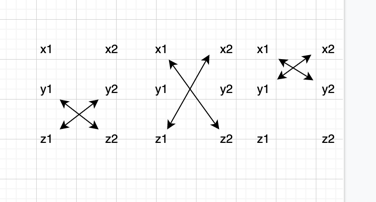
$img.png$ $img.png$

计算顺序：y、z、x

几何解释

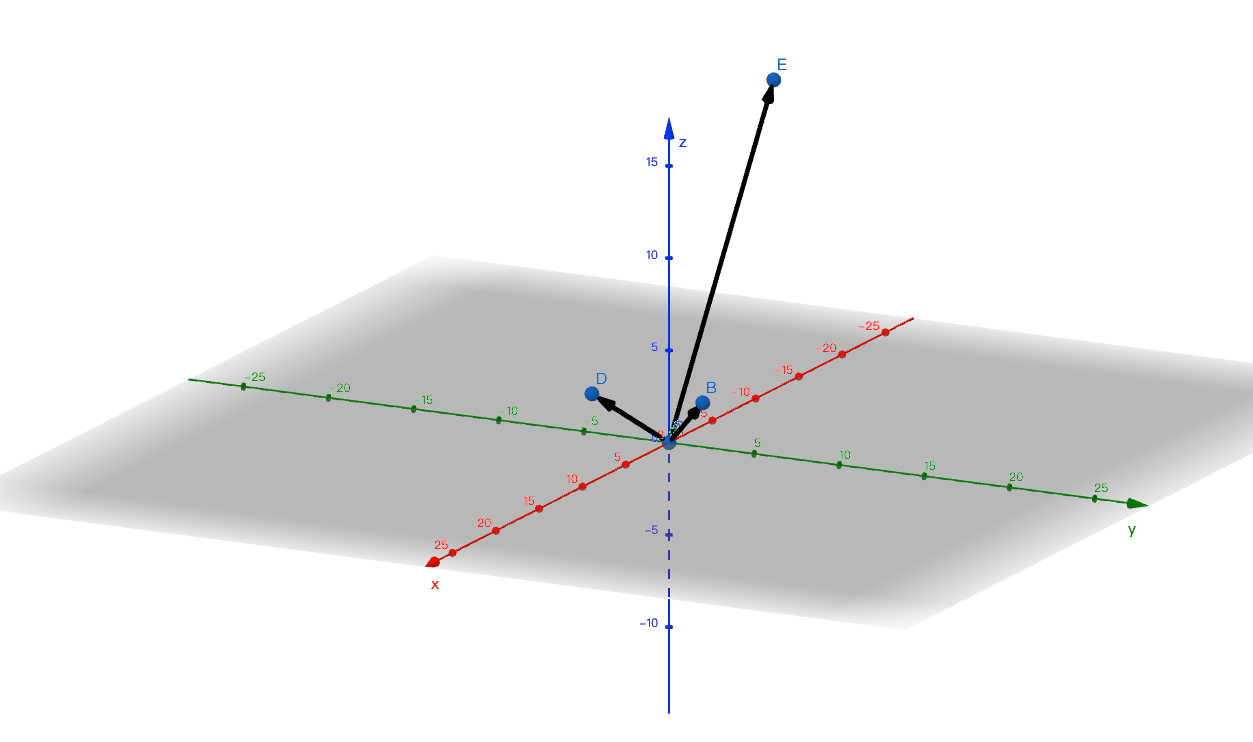
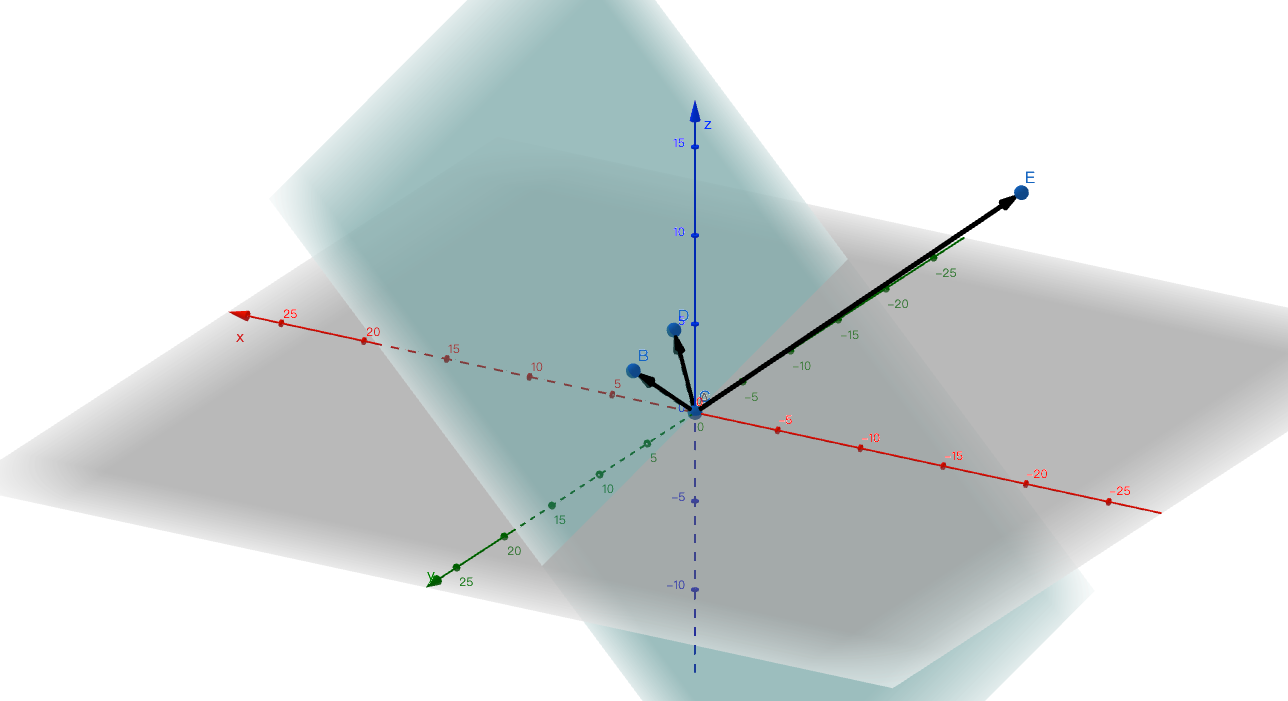
叉乘得到的向量是垂直于向量a、向量b所在的平面 $img.png$

$img.png$

叉乘向量的长度值等于向量a、向量b构成平行四边形的面积值
几何计算公式，n向量为向量a、向量b构成平面的单位向量

\vec{a} \times \vec{b} = | \begin{matrix} \vec{a} \end{matrix} | | \begin{matrix} \vec{b} \end{matrix} | \sin θ \vec{n}

根据几何意义可知，反交换律也就意味着交换后的乘积为转换符号后的面积值

x \times y + y \times x = 0

INFO

计算顺序：叉乘、点乘、乘除、加减

矩阵与线性变换

3D中的方位与角位移

四元数

代码实现

几何图元

几何检测

最近点

相交性检测

图形数学

可见行检测

向量

数学定义

几何定义

向量与点

向量运算

零向量

负向量

几何解释

长度

几何解释

标量与向量的乘积

几何解释

标准化

几何解释

加减规则

几何解释

点乘

几何解释

水平投影和垂直投影

叉乘

几何解释

四元数

最近点

相交性检测

向量 ​

数学定义 ​

几何定义 ​

向量与点 ​

向量运算 ​

零向量 ​

负向量 ​

几何解释 ​

长度 ​

几何解释 ​

标量与向量的乘积 ​

几何解释 ​

标准化 ​

几何解释 ​

加减规则 ​

几何解释 ​

点乘 ​

几何解释 ​

水平投影和垂直投影 ​

叉乘 ​

几何解释 ​

向量

数学定义

几何定义

向量与点

向量运算

零向量

负向量

几何解释

长度

几何解释

标量与向量的乘积

几何解释

标准化

几何解释

加减规则

几何解释

点乘

几何解释

水平投影和垂直投影

叉乘

几何解释