参数射线上的最近点

考虑2D和3D中的射线参数方程R：p( t ) = p_org + td

其中d为单位向量，表示射线的方向，参数t在0和l间变化，l是R的长度。我们要找出给定点q在射线R上的最近点q^'

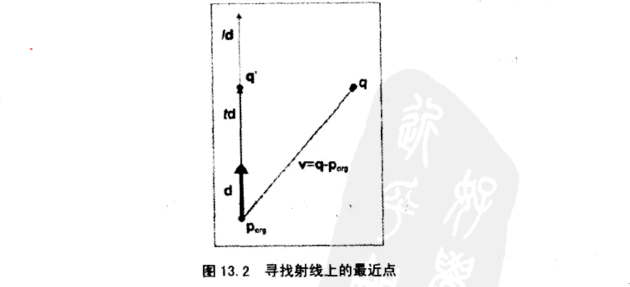
点乘v·d的结果就是满足p(t)=q^'的t值

$$t=d·v=d·(q-p_{org})$$$$q^{{}^{\prime }}=p(t)=p_{org}+td=p_{org}+(d·(q-p_{org}))d$$

以上是在t属于(0,l)间的最近点公式

• 当t<0时，R上距离q最近的点是起始点

• 当t>l时，R上距离q最近的点是终点（无穷远）

当射线的t是在0到1变化时，d不必是单位向量，那么在计算t时需要标准化

$$t=\frac{d·(q-p_{org})}{\Vert \begin{array}{c}d\end{array}\Vert }$$

INFO

为什么点乘v·d的结果就是满足p(t)=q^'的t值？

已知d为单位向量，那么

$$v·d=\Vert \begin{array}{c}v\end{array}\Vert \Vert \begin{array}{c}d\end{array}\Vert \cos \theta =\Vert \begin{array}{c}v\end{array}\Vert \cos \theta$$

最终结果是向量v在向量d上的投影，或者说在向量v平行于向量d的平行分量

那么在点q^'必然满足p( t ) = p_org + td

可以解释为：初始点加上t倍的d向量，而d又是单位向量，那么反推出

点乘v·d的结果就是满足p(t)=q^'的t值