3D中的方位与角位移

角位移表示为一个物体绕某一轴所转过的角度，它有大小、方向，单位为弧度，但一般不是向量

在3D中有3中方式可以用来描述方位：矩阵、欧拉角、四元数。

有一点p，距离原点距离为r，绕一固定在原点的轴旋转，旋转角度为θ，在极坐标中

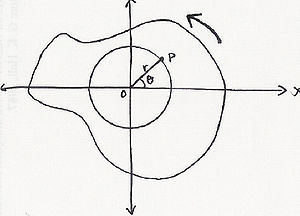
则角位移为：

$$s=\theta r\Rightarrow \theta =\frac{s}{r}$$

其中s为弧长

方位与方向

如果一个物体没有宽高，那么它只有方向而没有方位；反之，则既有方向又有方位

例如向量旋转时

有宽高的物体旋转时

描述物体的位置时不能使用绝对坐标，而是相对于某个特定坐标系下的相对位置。

同样，描述方位时也不能使用绝对坐标，而是以已知方位（如单位方位或源方位）为参考物来旋转，旋转的量为角位移。

方位与角位移

在数学上，描述方位和描述角位移是等价的，但是在本文中，我们严格区分方位、角位移、旋转。

将方位描述为一个单一的状态

将角位移想象为方向上的变换，两个状态之间的差异，例如从原方位到新方位，从物体坐标系到惯性坐标系。

具体来说，我们用矩阵和四元数表示“角位移”，用欧拉角表示“方位”

参考：

【1】角移