4x4齐次矩阵

齐次空间

在欧氏几何空间，同一平面的两条平行线不能相交；但是在透视空间中，同一平面的两条平行线是可以相交的。

欧氏几何空间可以看作是透视空间的一个子集，透视空间又可以称为齐次空间，用齐次坐标描述空间中的点。

用高维齐次空间描述低维欧式空间

在空间直角坐标系中，任意一点可用一个三维坐标矩阵[x y z]表示。如果将该点用一个四维坐标的矩阵[Hx Hy Hz H]表示时，则称为齐次坐标表示方法。在齐次坐标中，最后一维坐标H称为比例因子。

INFO

为什么要引入齐次坐标系？

我们已经知道可以通过矩阵乘法，将多个转换矩阵相乘来得到变换后的向量，但是只有平移是无法通过矩阵乘法计算的，在欧式空间中，它只能通过加减法计算

例如将向量v沿+x方向平移∆x，沿+y方向平移∆y，沿+z方向平移∆z，那么平移后的坐标为(x+∆x, y+∆y, z+∆z)

$${\mathrm{v}}^{{}^{\prime }}=\left[\begin{array}{ccc}x+\mathrm{\Delta }x& y+\mathrm{\Delta }y& z+\mathrm{\Delta }z\end{array}\right]$$

假设转换矩阵为M，我们依旧想通过矩阵乘法计算出转换矩阵M

$$\mathrm{v}·\mathrm{M}=\mathrm{v}+\mathrm{\Delta }\mathrm{t}$$

很明显是无法计算出M的，但是如果我们在增加一个维度分量w，则欧式3D空间中的点在齐次空间中表示为

$$\left[\begin{array}{ccc}x& y& z\end{array}\right]⟹\left[\begin{array}{cccc}x& y& z& w\end{array}\right]$$

转换为齐次空间，有

$$\left[\begin{array}{cccc}x& y& z& w\end{array}\right]·\left[\begin{array}{cccc}w& 0& 0& 0\\ 0& w& 0& 0\\ 0& 0& w& 0\\ \mathrm{\Delta }x& \mathrm{\Delta }y& \mathrm{\Delta }z& 1\end{array}\right]=\left[\begin{array}{cccc}wx+w\mathrm{\Delta }x& wy+w\mathrm{\Delta }y& wz+w\mathrm{\Delta }z& w\end{array}\right]$$

同时除以w，将齐次空间中的坐标换算为欧式3D空间中则有

$${\mathrm{v}}^{{}^{\prime }}=\left[\begin{array}{ccc}x+\mathrm{\Delta }x& y+\mathrm{\Delta }y& z+\mathrm{\Delta }z\end{array}\right]$$

因此为了方便起见，一般将w赋值为1

这样就把各种变换都统一了起来，都表示成一连串的矩阵相乘的形式，保证了形式上的一致。

2D、3D齐次空间

2D空间中的坐标描述为

$$(x,y)$$

3D齐次空间中的坐标则描述为

$$(x,y,w)$$

想象一个三维空间中z=w的平面，二维空间中的点是齐次空间中点在z=w平面上的投影

任意给定一个2D空间的点(x,y)，齐次空间中有无数个点与之对应，所有点的形式都是

$$(x,y,k),k\ne 0$$

当k=0时，将这个点解释为“无限远处的点”，对应欧式空间中的无穷大

3D、4D齐次空间

思想与2D中相同，将3D中的点理解为在4D齐次空间“平面”上的投影

3D空间中的坐标描述为

$$(x,y,z)$$

4D齐次空间中的坐标则描述为

$$(x,y,z,w)$$

相应的当k=0时，将这个点解释为“无限远处的点”

4x4平移矩阵

3x3矩阵是不包含平移的，而且任意矩阵乘法的变换都不包含平移，而通过引入4x4平移矩阵可以解决该问题。

将3x3转换矩阵扩展为4x4平移矩阵

$$\left[\begin{array}{ccc}{m}_{11}& m_{12}& m_{13}\\ m_{21}& m_{22}& m_{23}\\ m_{31}& m_{32}& m_{33}\end{array}\right]\Rightarrow \left[\begin{array}{cccc}{m}_{11}& m_{12}& m_{13}& 0\\ m_{21}& m_{22}& m_{23}& 0\\ m_{31}& m_{32}& m_{33}& 0\\ 0& 0& 0& 1\end{array}\right]$$

而且对于任意向量，矩阵乘法在欧式空间和齐次空间中的结果是相同的，只不过齐次空间多一个分量

$$\left[\begin{array}{ccc}x& y& z\end{array}\right]\left[\begin{array}{ccc}{m}_{11}& m_{12}& m_{13}\\ m_{21}& m_{22}& m_{23}\\ m_{31}& m_{32}& m_{33}\end{array}\right]$$$$=\left[\begin{array}{ccc}x{m}_{11}+y{m}_{21}+z{m}_{31}& x{m}_{12}+y{m}_{22}+z{m}_{32}& x{m}_{13}+y{m}_{23}+z{m}_{33}\end{array}\right]$$

暂时假设w=1，则有

$$\left[\begin{array}{cccc}x& y& z& 1\end{array}\right]\left[\begin{array}{cccc}{m}_{11}& m_{12}& m_{13}& 0\\ m_{21}& m_{22}& m_{23}& 0\\ m_{31}& m_{32}& m_{33}& 0\\ 0& 0& 0& 1\end{array}\right]$$$$=\left[\begin{array}{cccc}x{m}_{11}+y{m}_{21}+z{m}_{31}& x{m}_{12}+y{m}_{22}+z{m}_{32}& x{m}_{13}+y{m}_{23}+z{m}_{33}& 1\end{array}\right]$$

假如在最后一个行向量中引入偏移量，那么可以得到4x4平移矩阵

$$\left[\begin{array}{cccc}x& y& z& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ \mathrm{\Delta }x& \mathrm{\Delta }y& \mathrm{\Delta }z& 1\end{array}\right]=\left[\begin{array}{cccc}x+\mathrm{\Delta }x& y+\mathrm{\Delta }y& z+\mathrm{\Delta }z& 1\end{array}\right]$$

例如：一个向量通过旋转、平移得到新向量，旋转矩阵为R，平移矩阵为T则有

$$\begin{array}{rl}{\mathrm{v}}^{{}^{\prime }}& \\ & =\mathrm{v}RT& \\ & =\mathrm{v}\left[\begin{array}{cccc}{m}_{11}& m_{12}& m_{13}& 0\\ m_{21}& m_{22}& m_{23}& 0\\ m_{31}& m_{32}& m_{33}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ \mathrm{\Delta }x& \mathrm{\Delta }y& \mathrm{\Delta }z& 1\end{array}\right]& \\ & =\mathrm{v}\left[\begin{array}{cccc}{m}_{11}& m_{12}& m_{13}& 0\\ m_{21}& m_{22}& m_{23}& 0\\ m_{31}& m_{32}& m_{33}& 0\\ \mathrm{\Delta }x& \mathrm{\Delta }y& \mathrm{\Delta }z& 1\end{array}\right]\end{array}$$

为了更加明显的区分出旋转部分和平移部分信息，令

$$t=\left[\begin{array}{ccc}\mathrm{\Delta }x& \mathrm{\Delta }y& \mathrm{\Delta }z\end{array}\right]$$

则最终转换矩阵可以简化为

$$\left[\begin{array}{cc}R& 0\\ t& 1\end{array}\right]$$

一般仿射变换

在前文中我们探索了通过原点的任意轴、不包含平移的转换矩阵，在知道如何通过平移矩阵进行平移转换的前提下，我们探索三维空间下更一般的情况

• 绕不通过原点的任意轴旋转
• 沿不通过原点的任意轴缩放
• 向不通过原点的任意面正交投影
• 沿不通过原点的任意面镜像

其基本思想是将向量v先通过平移矩阵转换到原点处，再进行转换，最后在平移到原位置。其中平移矩阵为T，转换矩阵为R，平移逆矩阵为T^-1

$${\mathrm{v}}^{{}^{\prime }}=\mathrm{v}TR{T}^{-1}$$

最终的转换矩阵为

$$\begin{array}{rl}TR{T}^{-1}& \\ & =TR{T}^{-1}\\ & =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ -p_x& -p_y& -p_z& 1\end{array}\right]\left[\begin{array}{cccc}{m}_{11}& m_{12}& m_{13}& 0\\ m_{21}& m_{22}& m_{23}& 0\\ m_{31}& m_{32}& m_{33}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ p_x& p_y& p_z& 1\end{array}\right]\\ & =\left[\begin{array}{cc}I& 0\\ p& 1\end{array}\right]\left[\begin{array}{cc}R& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}I& 0\\ -p& 1\end{array}\right]\\ & =\left[\begin{array}{cc}R& 0\\ -pR+p& 1\end{array}\right]\end{array}$$

最终影响的只有最后一行，并没有影响线性变换矩阵。

透视投影

将物体投影到平面上，如果平面上的点与物体上的点连线之间是平行的则称为正交投影（又称为平行投影），如果相聚一点，则成为透视投影。

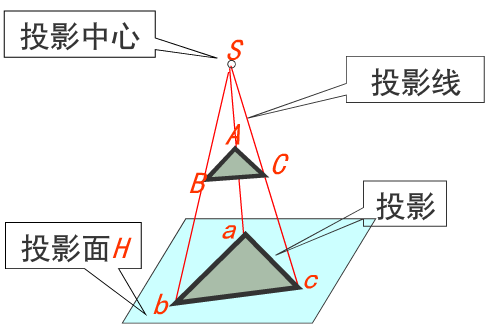
相交的那个点称为投影中心，投影平面在投影中心前面，因此会呈现出物体相对于投影中心越远则投影越小，越近则投影越大，简称为“近大远小”，这符合人类的视觉效果

INFO

透视投影是人类视觉系统的模型。

使用4x4矩阵进行透视投影

点p在z=d平面上进行透视投影，原点为投影中心，有

$$p^{{}^{\prime }}=\left[\begin{array}{ccc}\frac{d{p}_x}{p_z}& \frac{d{p}_y}{p_z}& d\end{array}\right]=\left[\begin{array}{ccc}{p}_x\frac{d}{p_z}& p_y\frac{d}{p_z}& p_z\frac{d}{p_z}\end{array}\right]$$

转换到四维齐次空间中，假设w=1，坐标表示为

$$\left[\begin{array}{cccc}{p}_x& p_y& p_z& \frac{p_z}{d}\end{array}\right]$$

考虑存在矩阵M将[p_x p_y p_z 1]转换为上述表达式

则在z=d平面上的投影矩阵为：

$$\left[\begin{array}{cccc}x& y& z& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& \frac{1}{d}\\ 0& 0& 0& 0\end{array}\right]=\left[\begin{array}{cccc}x& y& z& \frac{z}{d}\end{array}\right]$$

• 乘以这个矩阵实际并没有进行转换，它的作用只是用来计算出合适的分母
• 存在多种变化，矩阵不固定

小孔成像

在盒子上开一个孔，光线通过孔在盒子内部产生投影。将小孔处作为投影中心建立坐标系（左手坐标系）

从侧面看点p，投影面为z=-d，投影中心为原点，最终投影后的点为p^'

根据相似三角形可知

$$\frac{p_y}{p_z}=\frac{-p_y^{{}^{\prime }}}{d}\Rightarrow p_y^{{}^{\prime }}=-\frac{d{p}_y}{p_z}$$$$\frac{p_x}{p_z}=\frac{-p_x^{{}^{\prime }}}{d}\Rightarrow p_x^{{}^{\prime }}=-\frac{d{p}_x}{p_z}$$$$\frac{p_z}{p_z}=\frac{-p_x^{{}^{\prime }}}{d}\Rightarrow p_z^{{}^{\prime }}=-d$$

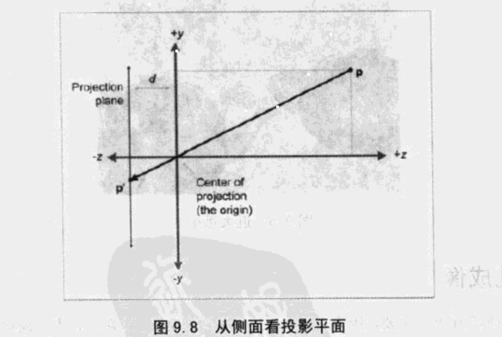
则点p在投影面为z=-d上的投影为

$$p^{{}^{\prime }}=\left[\begin{array}{c}{p}_x^{{}^{\prime }}\\ p_y^{{}^{\prime }}\\ p_z^{{}^{\prime }}\end{array}\right]=\left[\begin{array}{c}-\frac{d{p}_x}{p_z}\\ -\frac{d{p}_y}{p_z}\\ -d\end{array}\right]$$

相应的在z=d平面上的投影为

$$p^{{}^{\prime }}=\left[\begin{array}{c}{p}_x^{{}^{\prime }}\\ p_y^{{}^{\prime }}\\ p_z^{{}^{\prime }}\end{array}\right]=\left[\begin{array}{c}\frac{d{p}_x}{p_z}\\ \frac{d{p}_y}{p_z}\\ d\end{array}\right]$$

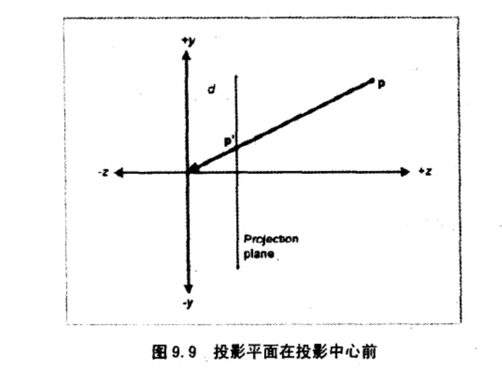
这样可以降低计算的复杂度，但是这种小孔成像在真实世界是不存在的

INFO

小孔成像是摄像机的模型。

参考：

【1】关于齐次坐标的理解